Add Shamir's Secret Sharing notes, update templates

README.md

@@ -3,7 +3,8 @@
 https://arnaucube.com/blog
 
 ## Usage
+- Install [blogo](https://github.com/arnaucube/blogo)
 - Edit the files from `/blogo-input`
-- Execute `./blogo` to generate the html files
+- Execute `blogo` to generate the html files
 
 More details: https://github.com/arnaucube/blogo

blogo-input/blogo.json

@@ -8,6 +8,11 @@
   "metadescr": "arnaucube blog",
   "metaimg": "img/logoArnauCube.png",
   "posts": [
+    {
+      "thumb": "shamir-secret-sharing_thumb.md",
+      "md": "shamir-secret-sharing.md",
+      "metadescr": ""
+    },
     {
       "thumb": "kzg-batch-proof_thumb.md",
       "md": "kzg-batch-proof.md",

blogo-input/index.html

@@ -127,6 +127,22 @@
         console.log(theme);
       }
     </script>
+  <script>
+    function tagLinks(tagName) {
+      var tags = document.getElementsByTagName(tagName);
+      for (var i=0, hElem; hElem =  tags[i]; i++) {
+        if (hElem.parentNode.className=="row postThumb") {
+          continue;
+        }
+        hElem.id = hElem.innerHTML.toLowerCase().replace(" ", "-");
+        hElem.innerHTML = "<a style='text-decoration:none;color:black;' href='#"+hElem.id+"'>"+hElem.innerHTML+"</a>";
+      }
+    }
+    tagLinks("h2");
+    tagLinks("h3");
+    tagLinks("h4");
+    tagLinks("h5");
+    </script>
     <script src="https://cdn.jsdelivr.net/npm/mermaid/dist/mermaid.min.js"></script>
 
 

blogo-input/js/external-links.js

@@ -27,6 +27,10 @@ ready(function() {
   for (var i = 0; i < anchorElsLength; i++) {
     var anchorEl = anchorEls[i];
     var href = anchorEl.getAttribute('href');
+    if (href[0]=="#") {
+      // if its an internal link, do not add the 'target=_blank'
+      continue;
+    }
 
     if (!internalLinkRegex.test(href)) {
       anchorEl.setAttribute('target', '_blank');

blogo-input/posts/kzg-batch-proof.md

@@ -12,7 +12,7 @@ Let $(z_0, y_0), (z_1, y_1), ..., (z_k, y_k)$ be the points that we want to proo
 The *commitment* to the polynomial stands the same than for single proofs: $c=[p(\tau)]_1$.
 
 For the evaluation proof, while in the single proofs we compute $q(x) = \frac{p(x)-y}{x-z}$, we will replace $y$ and $x-z$ by the following two polynomials.
-The constant $y$ is replaced by a polynomial that has roots at all the points that we want to prove. This is achieved by computing the [Lagrange interpolation](https://en.wikipedia.org/wiki/Lagrange_polynomial) for the given set of points:
+The constant $y$ is replaced by a polynomial that has roots at all the points that we want to prove. This is achieved by computing the [Lagrange interpolation](/blog/shamir-secret-sharing.html#lagrange-polynomial%20interpolation) for the given set of points:
 
 $$
 I(x) = \sum_{j=0}^k y_j l_j(x)\newline

blogo-input/posts/kzg-commitments.md

@@ -81,3 +81,6 @@ We can see that is the equation $q(x)(x-z)=p(x)-y$, which can be expressed as $q
 The content covered in this notes is just a quick overview, but allows us to see the potential of the scheme. One next iteration from what we've seen is the approach to do batch proofs, which allows us to evaluate at multiple points with a single evaluation proof. This scheme can be used as a *vector commitment*, using a polynomial where the $p(i) = x_i$ for all values of $x_i$ of the vector, which can be obtained from the $x_i$ values and computing the [Lagrange interpolation](https://en.wikipedia.org/wiki/Lagrange_polynomial). This is quite useful combined with the mentioned batch proofs. The *batch proofs* logic can be found at the [blog/kzg-batch-proof](https://arnaucube.com/blog/kzg-batch-proof.html) notes (kind of the continuation of the current notes).
 
 As a final note, in order to try to digest the notes, I've did a *toy implementation* of this scheme at https://github.com/arnaucube/kzg-commitments-study. It's quite simple, but contains the logic overviewed in this notes.
+
+<br>
+- [Part 2: Batch proof in KZG Commitments](https://arnaucube.com/blog/kzg-batch-proof.html)

blogo-input/posts/kzg-commitments_thumb.md

@@ -2,4 +2,3 @@
 In the following notes I've tried to summarize the KZG Commitments scheme with the concepts that helped me to follow the reasoning.
 
 *2021-08-05*
-

blogo-input/posts/shamir-secret-sharing.md

@@ -0,0 +1,89 @@
+## Lagrange Polynomial Interpolation and Shamir secret sharing
+*2021-10-10*
+
+> If you read this post, be aware that I’m not a mathematician, I’m just an amateur on math studying in my free time, and this article is just an attempt to try to sort the notes that I took while learning about Lagrange polynomial interpolation and Shamir's secret sharing.
+
+Imagine that you have a *secret* (for example a *private key* that can decrypt a file), and you want to backup that *secret*. You can split the *secret* and give each slice to a different person, so when you need to reconstruct the *secret* you just need to put together all the parts. But, what happens if one of the parts gets corrupted, or is lost? The secret would not be recoverable.
+A better solution can be done if we use *Shamir Secret Sharing*, which allows us to split the *secret* in $k$ different parts, and set a minimum threshold $n$, which defines the number of required parts to recover the *secret*, so just by putting together any $n$ parts we will recover the original secret.
+
+This has interesting applications, such as social recovery of keys or distributing a secret and ensuring that cooperation is needed in order to recover it. In the following lines we will overview the concepts behind this scheme.
+
+### Lagrange polynomial interpolation
+Lagrange interpolation is also used in many schemes that work with polynomials, for example in [KZG Commitments](https://arnaucube.com/blog/kzg-batch-proof.html) (an actual implementation [can be found here](https://github.com/arnaucube/kzg-commitments-study/blob/master/arithmetic.go#L272)).
+
+The main idea behind is the following: for any $n$ distinct points over $\mathbb{R}^2$, there is a unique polynomial $p(x) \in \mathbb{R[x]}$ of degree $n-1$ which goes through all of them.
+From the 'other side' point of view, this means that if we have a polynomial of degree $n-1$, we can take $n$ points (or more) from it, and we will be able to recover the original polynomial from those $n$ points.
+
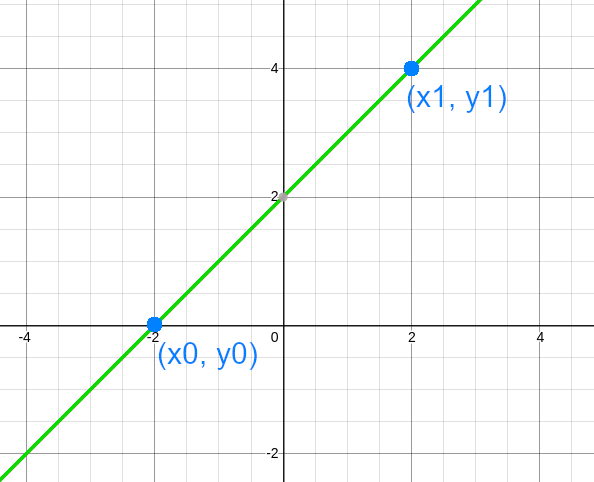
+We can see this starting with a line. If we are given any two points $P_0=(x_0, y_0)$ and $P_1=(x_1, y_1)$ from that line, we are able to recover the original line.
+
+<div style="text-align:center;">
+    <img style="width:300px;margin-bottom:20px;" src="img/posts/shamir-secret-sharing/line.png" />
+</div>
+
+
+We can map this into the previous idea, seeing that our line is a degree $1$ polynomial, so, if we pick $2$ points from it, we later can recover the original line.
+
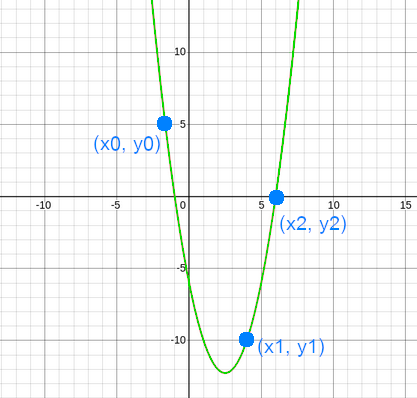
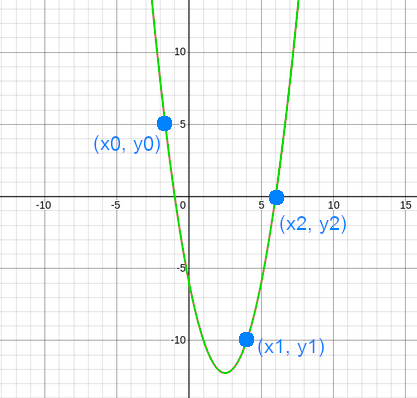
+Same happens with polynomials of degree $2$. Let $p(x)$ be a polynomial of degree $2$ defined by $p(x)= x^2 - 5x - 6$. We can create infinity of polynomials of degree $2$ that go through $2$ points, but with 3 points there is a unique polynomial degree $2$
+
+As the degree is $2$, if we pick $3$ points from the polynomial, we will be able to reconstruct it.
+<div style="text-align:center;">
+    <img style="width:300px;margin-bottom:20px;" src="img/posts/shamir-secret-sharing/degree2.png" />
+</div>
+
+This is generalized by using *Lagrange polynomial interpolation*, which defines:
+
+For a set of points $(x_0, y_0), (x_1, y_1), ..., (x_n, x_n)$,
+
+$$
+I(x) = \sum_{i=0}^n y_i l_i(x)\newline
+where \space\space\space l_i(x) = \prod\_{0\leq j \leq n, j\neq i} \frac{x-x_j}{x_i - x_j}
+$$
+
+
+### Shamir's secret sharing
+As we've seen, for a degree $n-1$ polynomial we can pick $n$ or more points and we will be able to reconstruct the original polynomial from it. This is the main idea used in *Shamir's secret sharing*.
+
+Let $s$ be our secret. We want to generate $k$ pieces and set a threshold $n$ which is the minimum number of pieces that are needed to reconstruct the secret $s$. We can define a polynomial of degree $n-1$, and pick $k$ points from that polynomial, so in this way with just putting together $n$ points of $k$ we will be able to reconstruct the original polynomial. And, we can place our secret $s$ in the *constant term* of the polynomial (the one that has $x^0$), in this way, when we reconstruct the polynomial using $n$ out of $k$ points, we will be able to recover the secret $s$.
+
+We can see this with an example with actual numbers (we will use small numbers):
+Imagine that we want to generate $5$ pieces from our secret, and define that just by putting together $3$ of the pieces we can recover the secret, this means setting $n=3$ and $k=5$. Then we will generate a polynomial of degree $n-1=2$, by $p(x) = \alpha_0 + \alpha_1 x  + \alpha_2 x^2$, where $\alpha_0 = s$ (the secret).
+
+We will work over a finite field of size $p$, where $p$ is a prime number. For our example we will work over $\mathbb{F}_{19}$, in real world we would work with much more bigger field. You can find an [example without finite fields in Wikipedia](https://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing#Example).
+
+Let our secret be $s=14$. We now generate our polynomial of degree $n-1=2$, where $s$ will be the constant coefficient: $p(x)= s + \alpha_1 x^1 + \alpha_2 x^2$. We can set $\alpha_1$ and $\alpha_2$ into any random value, as example $\alpha_1=4$ and $\alpha_2=6$. So we have our polynomial: $p(x) = 14 + 4 x + 6 x^2$.
+
+Now that we have the polynomial, we can pick $k$ points from it, using incremental indexes for the $x$ coordinate: $P_1=(1, p(1)), P_2=(2, p(2)), \space\ldots\space, P_k=(k, p(k))$. With the numbers of our example this is (remember, we work over $\mathbb{F}\_{19}$):
+$$
+p(x) = 14 + 4 x + 6 x^2,\newline
+p(1)=14 + 4 \cdot 1 + 6 \cdot 1^2 = 24 \space (mod \space 19) = 5\newline
+p(2)=14 + 4 \cdot 2 + 6 \cdot 2^2 = 46 \space (mod \space 19) = 8\newline
+p(3)=14 + 4 \cdot 3 + 6 \cdot 3^2 = 80 \space (mod \space 19) = 4\newline
+p(4)=14 + 4 \cdot 4 + 6 \cdot 4^2 = 126 \space (mod \space 19) = 12\newline
+p(5)=14 + 4 \cdot 5 + 6 \cdot 5^2 = 184 \space (mod \space 19) = 13
+$$
+So our $k$ points are: $(1,5), (2,8), (3,4), (4,12), (5,13)$. We can distribute these points as our 'secret parts'.
+In order to recover the secret, we need at least $n=3$ points, for example $P_1$, $P_3$, $P_5$, and we compute the *Lagrange polynomial interpolation* to recover the original polynomial (remember, we work over $\mathbb{F}\_{19}$):
+
+$$
+I(x) = \sum_{i=0}^n y_i l_i(x) \space\space
+where \space\space\space l_i(x) = \prod\_{0 \leq j \leq n \\ j\neq i} \frac{x-x_j}{x_i - x_j}
+$$
+$$
+l_1(x) = \frac{x-3}{1-3} \cdot \frac{x-5}{1-5} = \frac{x-3}{17} \cdot \frac{x-5}{15}=\frac{x^2+11x+15}{8}\newline
+l_3(x) = \frac{x-1}{3-1} \cdot \frac{x-5}{3-5} = \frac{x-1}{2} \cdot \frac{x-5}{17} =\frac{x^2+13x+5}{15}\newline
+l_5(x) = \frac{x-1}{5-1} \cdot \frac{x-3}{5-3} = \frac{x-1}{4} \cdot \frac{x-3}{2} = \frac{x^2 + 15x + 3}{8}\newline
+$$
+$$
+I(x) = y_2 \cdot l_2(x) + y_4 \cdot l_4(x) + y_5 \cdot l_5(x)\newline
+= 5 \cdot (\frac{x^2+11x+15}{8}) + 4 \cdot (\frac{x^2+13x+5}{15}) + 13 \cdot (\frac{x^2 +15x + 3}{8})\newline
+= \frac{5x^2+17x+18}{8} + \frac{4x^2+14x+1}{15} + \frac{13x^2+5x+1}{8}\newline
+= 3x^2+14x+7 + 18x^2+6x+14 + 4x^2+3x+12\newline
+= 6x^2 + 4x + 14
+$$
+
+We can now take the *constant coefficient*, or just evaluate the obtained polynomial at 0, $p(0) = 6 \cdot 0^2 + 4 \cdot 0 + 14 = 14$, and we obtain our original secret $s=14$.
+
+### Conclusions
+As an example of an use case of *Shamir Secret Sharing* we can think of social recovery of keys, there is an useful implementation of this scheme is used in the [banana split by Parity](https://bs.parity.io/). Also, here it is an implementation of the scheme in `Go`&`Rust` done a couple of years ago: https://github.com/arnaucube/shamirsecretsharing.
+
+*Lagrange Interpolation* in its own way, is a very useful tool in many schemes, it is also used in KZG Commitments, in zkSNARKs, zkSTARKs, PLONK, etc. In most of the schemes where polynomials are involved it becomes a very useful tool.

blogo-input/posts/shamir-secret-sharing_thumb.md

@@ -0,0 +1,4 @@
+### Lagrange Polynomial Interpolation and Shamir secret sharing
+Overview of Langrange Polynomial interpolation and Shamir's secret sharing.
+
+*2021-10-10*

public/blind-signatures-ec.html

@@ -233,6 +233,22 @@ func main() {
         console.log(theme);
       }
     </script>
+  <script>
+    function tagLinks(tagName) {
+      var tags = document.getElementsByTagName(tagName);
+      for (var i=0, hElem; hElem =  tags[i]; i++) {
+        if (hElem.parentNode.className=="row postThumb") {
+          continue;
+        }
+        hElem.id = hElem.innerHTML.toLowerCase().replace(" ", "-");
+        hElem.innerHTML = "<a style='text-decoration:none;color:black;' href='#"+hElem.id+"'>"+hElem.innerHTML+"</a>";
+      }
+    }
+    tagLinks("h2");
+    tagLinks("h3");
+    tagLinks("h4");
+    tagLinks("h5");
+    </script>
     <script src="https://cdn.jsdelivr.net/npm/mermaid/dist/mermaid.min.js"></script>
 
 

public/blogo.html

@@ -480,6 +480,22 @@ func putHTMLToTemplate(template string, m map[string]string) string {
         console.log(theme);
       }
     </script>
+  <script>
+    function tagLinks(tagName) {
+      var tags = document.getElementsByTagName(tagName);
+      for (var i=0, hElem; hElem =  tags[i]; i++) {
+        if (hElem.parentNode.className=="row postThumb") {
+          continue;
+        }
+        hElem.id = hElem.innerHTML.toLowerCase().replace(" ", "-");
+        hElem.innerHTML = "<a style='text-decoration:none;color:black;' href='#"+hElem.id+"'>"+hElem.innerHTML+"</a>";
+      }
+    }
+    tagLinks("h2");
+    tagLinks("h3");
+    tagLinks("h4");
+    tagLinks("h5");
+    </script>
     <script src="https://cdn.jsdelivr.net/npm/mermaid/dist/mermaid.min.js"></script>
 
 

public/coffeeminer-hacking-wifi-cryptocurrency-miner.html

@@ -619,6 +619,22 @@ def start():
         console.log(theme);
       }
     </script>
+  <script>
+    function tagLinks(tagName) {
+      var tags = document.getElementsByTagName(tagName);
+      for (var i=0, hElem; hElem =  tags[i]; i++) {
+        if (hElem.parentNode.className=="row postThumb") {
+          continue;
+        }
+        hElem.id = hElem.innerHTML.toLowerCase().replace(" ", "-");
+        hElem.innerHTML = "<a style='text-decoration:none;color:black;' href='#"+hElem.id+"'>"+hElem.innerHTML+"</a>";
+      }
+    }
+    tagLinks("h2");
+    tagLinks("h3");
+    tagLinks("h4");
+    tagLinks("h5");
+    </script>
     <script src="https://cdn.jsdelivr.net/npm/mermaid/dist/mermaid.min.js"></script>
 
 

public/flock-botnet.html

@@ -405,6 +405,22 @@
         console.log(theme);
       }
     </script>
+  <script>
+    function tagLinks(tagName) {
+      var tags = document.getElementsByTagName(tagName);
+      for (var i=0, hElem; hElem =  tags[i]; i++) {
+        if (hElem.parentNode.className=="row postThumb") {
+          continue;
+        }
+        hElem.id = hElem.innerHTML.toLowerCase().replace(" ", "-");
+        hElem.innerHTML = "<a style='text-decoration:none;color:black;' href='#"+hElem.id+"'>"+hElem.innerHTML+"</a>";
+      }
+    }
+    tagLinks("h2");
+    tagLinks("h3");
+    tagLinks("h4");
+    tagLinks("h5");
+    </script>
     <script src="https://cdn.jsdelivr.net/npm/mermaid/dist/mermaid.min.js"></script>
 
 

public/index.html

@@ -55,7 +55,16 @@
 
 
     <div class="container" style="margin-top:40px;max-width:800px;">
-      <a href='/blog/kzg-batch-proof.html'><div class="row postThumb">
+      <a href='/blog/shamir-secret-sharing.html'><div class="row postThumb">
+        <h3>Lagrange Polynomial Interpolation and Shamir secret sharing</h3>
+
+<p>Overview of Langrange Polynomial interpolation and Shamir&rsquo;s secret sharing.</p>
+
+<p><em>2021-10-10</em></p>
+
+</div>
+
+</a><a href='/blog/kzg-batch-proof.html'><div class="row postThumb">
         <h3>Batch proof in KZG Commitments</h3>
 
 <p>The benefit of <em>batch proof</em> is that allows us to proof multiple points while the proof size remains constant to one $\mathbb{G}_1$ point.</p>
@@ -181,6 +190,22 @@
         console.log(theme);
       }
     </script>
+  <script>
+    function tagLinks(tagName) {
+      var tags = document.getElementsByTagName(tagName);
+      for (var i=0, hElem; hElem =  tags[i]; i++) {
+        if (hElem.parentNode.className=="row postThumb") {
+          continue;
+        }
+        hElem.id = hElem.innerHTML.toLowerCase().replace(" ", "-");
+        hElem.innerHTML = "<a style='text-decoration:none;color:black;' href='#"+hElem.id+"'>"+hElem.innerHTML+"</a>";
+      }
+    }
+    tagLinks("h2");
+    tagLinks("h3");
+    tagLinks("h4");
+    tagLinks("h5");
+    </script>
     <script src="https://cdn.jsdelivr.net/npm/mermaid/dist/mermaid.min.js"></script>
 
 

public/js/external-links.js

@@ -27,6 +27,10 @@ ready(function() {
   for (var i = 0; i < anchorElsLength; i++) {
     var anchorEl = anchorEls[i];
     var href = anchorEl.getAttribute('href');
+    if (href[0]=="#") {
+      // if its an internal link, do not add the 'target=_blank'
+      continue;
+    }
 
     if (!internalLinkRegex.test(href)) {
       anchorEl.setAttribute('target', '_blank');

public/kzg-batch-proof.html

@@ -72,7 +72,7 @@ Let $(z_0, y_0), (z_1, y_1), …, (z_k, y_k)$ be the points that we want to
 The <em>commitment</em> to the polynomial stands the same than for single proofs: $c=[p(\tau)]_1$.</p>
 
 <p>For the evaluation proof, while in the single proofs we compute $q(x) = \frac{p(x)-y}{x-z}$, we will replace $y$ and $x-z$ by the following two polynomials.
-The constant $y$ is replaced by a polynomial that has roots at all the points that we want to prove. This is achieved by computing the <a href="https://en.wikipedia.org/wiki/Lagrange_polynomial">Lagrange interpolation</a> for the given set of points:</p>
+The constant $y$ is replaced by a polynomial that has roots at all the points that we want to prove. This is achieved by computing the <a href="/blog/shamir-secret-sharing.html#lagrange-polynomial%20interpolation">Lagrange interpolation</a> for the given set of points:</p>
 
 <p>$$
 I(x) = \sum_{j=0}^k y_j l_j(x)\newline
@@ -188,6 +188,22 @@ The problem with Merkle Trees is that the proof size grows linearly with the siz
         console.log(theme);
       }
     </script>
+  <script>
+    function tagLinks(tagName) {
+      var tags = document.getElementsByTagName(tagName);
+      for (var i=0, hElem; hElem =  tags[i]; i++) {
+        if (hElem.parentNode.className=="row postThumb") {
+          continue;
+        }
+        hElem.id = hElem.innerHTML.toLowerCase().replace(" ", "-");
+        hElem.innerHTML = "<a style='text-decoration:none;color:black;' href='#"+hElem.id+"'>"+hElem.innerHTML+"</a>";
+      }
+    }
+    tagLinks("h2");
+    tagLinks("h3");
+    tagLinks("h4");
+    tagLinks("h5");
+    </script>
     <script src="https://cdn.jsdelivr.net/npm/mermaid/dist/mermaid.min.js"></script>
 
 

public/kzg-commitments.html

@@ -147,6 +147,9 @@ $$
 
 <p>As a final note, in order to try to digest the notes, I&rsquo;ve did a <em>toy implementation</em> of this scheme at <a href="https://github.com/arnaucube/kzg-commitments-study">https://github.com/arnaucube/kzg-commitments-study</a>. It&rsquo;s quite simple, but contains the logic overviewed in this notes.</p>
 
+<p><br>
+- <a href="https://arnaucube.com/blog/kzg-batch-proof.html">Part 2: Batch proof in KZG Commitments</a></p>
+
     </div>
 
     <footer style="text-align:center; margin-top:100px;margin-bottom:50px;">
@@ -218,6 +221,22 @@ $$
         console.log(theme);
       }
     </script>
+  <script>
+    function tagLinks(tagName) {
+      var tags = document.getElementsByTagName(tagName);
+      for (var i=0, hElem; hElem =  tags[i]; i++) {
+        if (hElem.parentNode.className=="row postThumb") {
+          continue;
+        }
+        hElem.id = hElem.innerHTML.toLowerCase().replace(" ", "-");
+        hElem.innerHTML = "<a style='text-decoration:none;color:black;' href='#"+hElem.id+"'>"+hElem.innerHTML+"</a>";
+      }
+    }
+    tagLinks("h2");
+    tagLinks("h3");
+    tagLinks("h4");
+    tagLinks("h5");
+    </script>
     <script src="https://cdn.jsdelivr.net/npm/mermaid/dist/mermaid.min.js"></script>
 
 

public/shamir-secret-sharing.html

@@ -0,0 +1,244 @@
+<!DOCTYPE html>
+<html lang="en">
+
+  <head>
+    <meta name="description" content="" />
+    <meta charset="utf-8">
+    <title> Lagrange Polynomial Interpolation and Shamir secret sharing - arnaucube - blog</title>
+    <meta name="title" content=" Lagrange Polynomial Interpolation and Shamir secret sharing - arnaucube - blog">
+    <meta name="description" content="">
+
+    <meta property="og:title" content=" Lagrange Polynomial Interpolation and Shamir secret sharing - arnaucube - blog" />
+    <meta property="og:description" content="" />
+    <meta property="og:url" content="https://arnaucube.com/blog/shamir-secret-sharing.html" />
+    <meta property="og:type" content="article" />
+    <meta property="og:image" content="https://arnaucube.com/blog/" />
+    <meta name="twitter:title" content=" Lagrange Polynomial Interpolation and Shamir secret sharing - arnaucube - blog">
+    <meta name="twitter:description" content="">
+    <meta name="twitter:image" content="https://arnaucube.com/blog/">
+    <meta name="twitter:card" content="summary_large_image">
+    <meta name="author" content="arnaucube">
+
+    <meta name="viewport" content="width=device-width, initial-scale=1">
+
+    <link href="https://cdn.jsdelivr.net/npm/bootstrap@5.0.2/dist/css/bootstrap.min.css" rel="stylesheet" integrity="sha384-EVSTQN3/azprG1Anm3QDgpJLIm9Nao0Yz1ztcQTwFspd3yD65VohhpuuCOmLASjC" crossorigin="anonymous">
+    <link rel="stylesheet" href="css/style.css">
+
+    <!-- highlightjs -->
+    <!-- <link rel="stylesheet" href="js/highlightjs/atom-one-dark.css"> -->
+    <link rel="stylesheet" href="js/highlightjs/gruvbox-dark.css">
+    <script src="js/highlightjs/highlight.pack.js"></script>
+
+    <!-- katex -->
+    <link rel="stylesheet" href="https://cdn.jsdelivr.net/npm/katex@0.13.11/dist/katex.min.css" integrity="sha384-Um5gpz1odJg5Z4HAmzPtgZKdTBHZdw8S29IecapCSB31ligYPhHQZMIlWLYQGVoc" crossorigin="anonymous">
+  </head>
+
+  <body>
+
+    <!-- o_gradient_background" -->
+    <nav id="mainNav" class="navbar navbar-default navbar-fixed-top"
+                      style="height:50px;font-size:130%;">
+      <div class="container">
+        <a href="/blog" style="color:#000;">Blog index</a>
+        <div style="float:right;">
+          <a href="/" style="color:#000;display:inline-block;">arnaucube.com</a>
+          <div class="onoffswitch" style="margin:10px;display:inline-block;" title="change theme">
+            <input onclick="switchTheme()" type="checkbox" name="onoffswitch" class="onoffswitch-checkbox"
+              id="themeSwitcher">
+            <label class="onoffswitch-label" for="themeSwitcher"></label>
+          </div>
+        </div>
+      </div>
+      <img style="height:5px; width:100%; margin-top:8px;" src="img/gradient-line.jpg" />
+    </nav>
+
+
+
+    <div class="container" style="margin-top:40px;max-width:800px;">
+      <h2>Lagrange Polynomial Interpolation and Shamir secret sharing</h2>
+
+<p><em>2021-10-10</em></p>
+
+<blockquote>
+<p>If you read this post, be aware that I’m not a mathematician, I’m just an amateur on math studying in my free time, and this article is just an attempt to try to sort the notes that I took while learning about Lagrange polynomial interpolation and Shamir&rsquo;s secret sharing.</p>
+</blockquote>
+
+<p>Imagine that you have a <em>secret</em> (for example a <em>private key</em> that can decrypt a file), and you want to backup that <em>secret</em>. You can split the <em>secret</em> and give each slice to a different person, so when you need to reconstruct the <em>secret</em> you just need to put together all the parts. But, what happens if one of the parts gets corrupted, or is lost? The secret would not be recoverable.
+A better solution can be done if we use <em>Shamir Secret Sharing</em>, which allows us to split the <em>secret</em> in $k$ different parts, and set a minimum threshold $n$, which defines the number of required parts to recover the <em>secret</em>, so just by putting together any $n$ parts we will recover the original secret.</p>
+
+<p>This has interesting applications, such as social recovery of keys or distributing a secret and ensuring that cooperation is needed in order to recover it. In the following lines we will overview the concepts behind this scheme.</p>
+
+<h3>Lagrange polynomial interpolation</h3>
+
+<p>Lagrange interpolation is also used in many schemes that work with polynomials, for example in <a href="https://arnaucube.com/blog/kzg-batch-proof.html">KZG Commitments</a> (an actual implementation <a href="https://github.com/arnaucube/kzg-commitments-study/blob/master/arithmetic.go#L272">can be found here</a>).</p>
+
+<p>The main idea behind is the following: for any $n$ distinct points over $\mathbb{R}^2$, there is a unique polynomial $p(x) \in \mathbb{R[x]}$ of degree $n-1$ which goes through all of them.
+From the &lsquo;other side&rsquo; point of view, this means that if we have a polynomial of degree $n-1$, we can take $n$ points (or more) from it, and we will be able to recover the original polynomial from those $n$ points.</p>
+
+<p>We can see this starting with a line. If we are given any two points $P_0=(x_0, y_0)$ and $P_1=(x_1, y_1)$ from that line, we are able to recover the original line.</p>
+
+<div style="text-align:center;">
+    <img style="width:300px;margin-bottom:20px;" src="img/posts/shamir-secret-sharing/line.png" />
+</div>
+
+<p>We can map this into the previous idea, seeing that our line is a degree $1$ polynomial, so, if we pick $2$ points from it, we later can recover the original line.</p>
+
+<p>Same happens with polynomials of degree $2$. Let $p(x)$ be a polynomial of degree $2$ defined by $p(x)= x^2 - 5x - 6$. We can create infinity of polynomials of degree $2$ that go through $2$ points, but with 3 points there is a unique polynomial degree $2$</p>
+
+<p>As the degree is $2$, if we pick $3$ points from the polynomial, we will be able to reconstruct it.
+<div style="text-align:center;">
+    <img style="width:300px;margin-bottom:20px;" src="img/posts/shamir-secret-sharing/degree2.png" />
+</div></p>
+
+<p>This is generalized by using <em>Lagrange polynomial interpolation</em>, which defines:</p>
+
+<p>For a set of points $(x_0, y_0), (x_1, y_1), &hellip;, (x_n, x_n)$,</p>
+
+<p>$$
+I(x) = \sum_{i=0}^n y_i l_i(x)\newline
+where \space\space\space l_i(x) = \prod_{0\leq j \leq n, j\neq i} \frac{x-x_j}{x_i - x_j}
+$$</p>
+
+<h3>Shamir&rsquo;s secret sharing</h3>
+
+<p>As we&rsquo;ve seen, for a degree $n-1$ polynomial we can pick $n$ or more points and we will be able to reconstruct the original polynomial from it. This is the main idea used in <em>Shamir&rsquo;s secret sharing</em>.</p>
+
+<p>Let $s$ be our secret. We want to generate $k$ pieces and set a threshold $n$ which is the minimum number of pieces that are needed to reconstruct the secret $s$. We can define a polynomial of degree $n-1$, and pick $k$ points from that polynomial, so in this way with just putting together $n$ points of $k$ we will be able to reconstruct the original polynomial. And, we can place our secret $s$ in the <em>constant term</em> of the polynomial (the one that has $x^0$), in this way, when we reconstruct the polynomial using $n$ out of $k$ points, we will be able to recover the secret $s$.</p>
+
+<p>We can see this with an example with actual numbers (we will use small numbers):
+Imagine that we want to generate $5$ pieces from our secret, and define that just by putting together $3$ of the pieces we can recover the secret, this means setting $n=3$ and $k=5$. Then we will generate a polynomial of degree $n-1=2$, by $p(x) = \alpha_0 + \alpha_1 x  + \alpha_2 x^2$, where $\alpha_0 = s$ (the secret).</p>
+
+<p>We will work over a finite field of size $p$, where $p$ is a prime number. For our example we will work over $\mathbb{F}_{19}$, in real world we would work with much more bigger field. You can find an <a href="https://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing#Example">example without finite fields in Wikipedia</a>.</p>
+
+<p>Let our secret be $s=14$. We now generate our polynomial of degree $n-1=2$, where $s$ will be the constant coefficient: $p(x)= s + \alpha_1 x^1 + \alpha_2 x^2$. We can set $\alpha_1$ and $\alpha_2$ into any random value, as example $\alpha_1=4$ and $\alpha_2=6$. So we have our polynomial: $p(x) = 14 + 4 x + 6 x^2$.</p>
+
+<p>Now that we have the polynomial, we can pick $k$ points from it, using incremental indexes for the $x$ coordinate: $P_1=(1, p(1)), P_2=(2, p(2)), \space\ldots\space, P_k=(k, p(k))$. With the numbers of our example this is (remember, we work over $\mathbb{F}_{19}$):
+$$
+p(x) = 14 + 4 x + 6 x^2,\newline
+p(1)=14 + 4 \cdot 1 + 6 \cdot 1^2 = 24 \space (mod \space 19) = 5\newline
+p(2)=14 + 4 \cdot 2 + 6 \cdot 2^2 = 46 \space (mod \space 19) = 8\newline
+p(3)=14 + 4 \cdot 3 + 6 \cdot 3^2 = 80 \space (mod \space 19) = 4\newline
+p(4)=14 + 4 \cdot 4 + 6 \cdot 4^2 = 126 \space (mod \space 19) = 12\newline
+p(5)=14 + 4 \cdot 5 + 6 \cdot 5^2 = 184 \space (mod \space 19) = 13
+$$
+So our $k$ points are: $(1,5), (2,8), (3,4), (4,12), (5,13)$. We can distribute these points as our &lsquo;secret parts&rsquo;.
+In order to recover the secret, we need at least $n=3$ points, for example $P_1$, $P_3$, $P_5$, and we compute the <em>Lagrange polynomial interpolation</em> to recover the original polynomial (remember, we work over $\mathbb{F}_{19}$):</p>
+
+<p>$$
+I(x) = \sum_{i=0}^n y_i l_i(x) \space\space
+where \space\space\space l_i(x) = \prod_{0 \leq j \leq n \ j\neq i} \frac{x-x_j}{x_i - x_j}
+$$
+$$
+l_1(x) = \frac{x-3}{1-3} \cdot \frac{x-5}{1-5} = \frac{x-3}{17} \cdot \frac{x-5}{15}=\frac{x^2+11x+15}{8}\newline
+l_3(x) = \frac{x-1}{3-1} \cdot \frac{x-5}{3-5} = \frac{x-1}{2} \cdot \frac{x-5}{17} =\frac{x^2+13x+5}{15}\newline
+l_5(x) = \frac{x-1}{5-1} \cdot \frac{x-3}{5-3} = \frac{x-1}{4} \cdot \frac{x-3}{2} = \frac{x^2 + 15x + 3}{8}\newline
+$$
+$$
+I(x) = y_2 \cdot l_2(x) + y_4 \cdot l_4(x) + y_5 \cdot l_5(x)\newline
+= 5 \cdot (\frac{x^2+11x+15}{8}) + 4 \cdot (\frac{x^2+13x+5}{15}) + 13 \cdot (\frac{x^2 +15x + 3}{8})\newline
+= \frac{5x^2+17x+18}{8} + \frac{4x^2+14x+1}{15} + \frac{13x^2+5x+1}{8}\newline
+= 3x^2+14x+7 + 18x^2+6x+14 + 4x^2+3x+12\newline
+= 6x^2 + 4x + 14
+$$</p>
+
+<p>We can now take the <em>constant coefficient</em>, or just evaluate the obtained polynomial at 0, $p(0) = 6 \cdot 0^2 + 4 \cdot 0 + 14 = 14$, and we obtain our original secret $s=14$.</p>
+
+<h3>Conclusions</h3>
+
+<p>As an example of an use case of <em>Shamir Secret Sharing</em> we can think of social recovery of keys, there is an useful implementation of this scheme is used in the <a href="https://bs.parity.io/">banana split by Parity</a>. Also, here it is an implementation of the scheme in <code>Go</code>&amp;<code>Rust</code> done a couple of years ago: <a href="https://github.com/arnaucube/shamirsecretsharing">https://github.com/arnaucube/shamirsecretsharing</a>.</p>
+
+<p><em>Lagrange Interpolation</em> in its own way, is a very useful tool in many schemes, it is also used in KZG Commitments, in zkSNARKs, zkSTARKs, PLONK, etc. In most of the schemes where polynomials are involved it becomes a very useful tool.</p>
+
+    </div>
+
+    <footer style="text-align:center; margin-top:100px;margin-bottom:50px;">
+      <div class="container">
+        <div class="row">
+          <ul class="list-inline">
+            <li><a href="https://twitter.com/arnaucube"
+                   style="color:gray;text-decoration:none;"
+                   target="_blank">twitter.com/arnaucube</a>
+            </li>
+            <li><a href="https://github.com/arnaucube"
+                   style="color:gray;text-decoration:none;"
+                   target="_blank">github.com/arnaucube</a>
+            </li>
+          </ul>
+        </div>
+        <div class="row" style="display:inline-block;">
+          Blog made with <a href="http://github.com/arnaucube/blogo/"
+                            target="_blank" style="color: gray;text-decoration:none;">Blogo</a>
+        </div>
+      </div>
+    </footer>
+
+    <script>
+    </script>
+    <script src="js/external-links.js"></script>
+    <script>hljs.initHighlightingOnLoad();</script>
+    <script defer src="https://cdn.jsdelivr.net/npm/katex@0.13.11/dist/katex.min.js" integrity="sha384-YNHdsYkH6gMx9y3mRkmcJ2mFUjTd0qNQQvY9VYZgQd7DcN7env35GzlmFaZ23JGp" crossorigin="anonymous"></script>
+    <script defer src="https://cdn.jsdelivr.net/npm/katex@0.13.11/dist/contrib/auto-render.min.js" integrity="sha384-vZTG03m+2yp6N6BNi5iM4rW4oIwk5DfcNdFfxkk9ZWpDriOkXX8voJBFrAO7MpVl" crossorigin="anonymous"></script>
+    <script>
+      document.addEventListener("DOMContentLoaded", function() {
+        renderMathInElement(document.body, {
+          displayMode: false,
+          // customised options
+          // • auto-render specific keys, e.g.:
+          delimiters: [
+            {left: '$$', right: '$$', display: true},
+            {left: '$', right: '$', display: false},
+          ],
+          // • rendering keys, e.g.:
+          throwOnError : true
+        });
+      });
+
+      ///
+      let theme = localStorage.getItem("theme");
+      if ((theme === "light-theme")||(theme==null)) {
+          theme = "light-theme";
+          document.getElementById("themeSwitcher").checked = false;
+      } else if (theme === "dark-theme") {
+          theme = "dark-theme";
+          document.getElementById("themeSwitcher").checked = true;
+      }
+      document.body.className = theme;
+      localStorage.setItem("theme", theme);
+
+      function switchTheme() {
+        theme = localStorage.getItem("theme");
+        if (theme === "light-theme") {
+          theme = "dark-theme";
+          document.getElementById("themeSwitcher").checked = true;
+        } else {
+          theme = "light-theme";
+          document.getElementById("themeSwitcher").checked = false;
+        }
+        document.body.className = theme;
+        localStorage.setItem("theme", theme);
+
+        console.log(theme);
+      }
+    </script>
+  <script>
+    function tagLinks(tagName) {
+      var tags = document.getElementsByTagName(tagName);
+      for (var i=0, hElem; hElem =  tags[i]; i++) {
+        if (hElem.parentNode.className=="row postThumb") {
+          continue;
+        }
+        hElem.id = hElem.innerHTML.toLowerCase().replace(" ", "-");
+        hElem.innerHTML = "<a style='text-decoration:none;color:black;' href='#"+hElem.id+"'>"+hElem.innerHTML+"</a>";
+      }
+    }
+    tagLinks("h2");
+    tagLinks("h3");
+    tagLinks("h4");
+    tagLinks("h5");
+    </script>
+    <script src="https://cdn.jsdelivr.net/npm/mermaid/dist/mermaid.min.js"></script>
+
+
+  </body>
+</html>
+