Notes on blind signatures over elliptic curves
2021-07-30
Warning: I want to state clearly that I’m not a mathematician, I’m just an amateur on math studying in my free time, and this article is just an attempt to try to sort the notes that I took while reading about the blind signatures over elliptic curves.
Blind signatures
Few years ago I read about the RSA blind signatures scheme (thanks to Juan Hernández who discovered it to me) and I was amazed on such thing being possible. You can read the step by step of the RSA blind signatures scheme in this Wikipedia article. The main idea is that one party has a message and blinds it, then sends the blinded message to a signer. The signer generates a signature of that blinded message, who sends it to the initial party, who unblinds the signature, obtaining a valid signature for the original message, while the signer does not know what it is signing, but the signature can be verified for the original message for the signer’s public key.
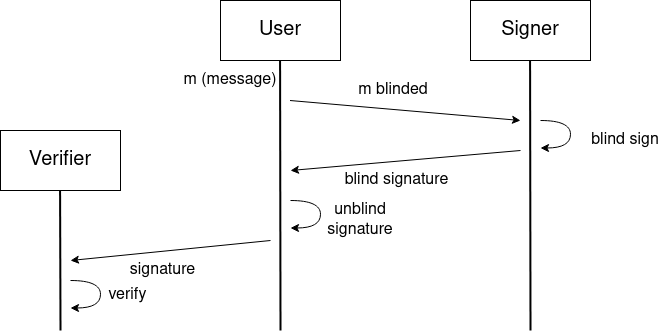 Diagram showing the described steps.
Diagram showing the described steps.
This has many applications, one of them could be to authenticate users in a ‘traditional’ way (by user&password, or by public key & signature) in the Certification Authority (CA), and once the user is authenticated, the user can create a new key pair (ephemeral key), for which public key gets blinded and sent to the CA. The CA performs a blind signature on it, and sends the result back to the user. Then, the user can unblind the signature, and as result has their public key signed by the CA, but the CA does not know which is the public key (but the CA knows that the user while being authenticated by their ‘traditional’ login, generated a new identity (key pair) and sent the public key blinded to the CA, who blindly signed it and returned the signature back to the user). Then the user has the ephemeral public key which is signed by the CA, and can use it to enter the system authenticating that they are an approved user without revealing which user they are.
As most of the current ongoing protocols are using elliptic curve cryptography instead of RSA, the mentioned RSA blind signatures scheme is not much plugable in the existing systems that use elliptic curve keys. That’s why I got interested into reading and learning about schemes that provide blind signatures over elliptic curve.
The scheme
In this notes, we will cover the scheme proposed at “New Blind Signature Schemes Based on the (Elliptic Curve) Discrete Logarithm Problem” paper by Hamid Mala & Nafiseh Nezhadansari (thanks to Daira Hopwood who mentioned this paper in a Telegram group).
First of all, the signer generates their key pair by generating a random scalar \(d \in \mathbb{Z}_n\) (where \(\mathbb{Z}_n\) is the elliptic curve field), which will be the private key. From \(d\) they can compute the public key by \(Q = dG\), where \(G\) is the generator point of \(\mathbb{G}\) (the elliptic curve group).
Appart from their key pair, the signer will generate for each request of signature another random value \(k \in \mathbb{Z}_n\), and its respective \(R'=kG\).
The user has a message m that which they want to get signed by the signer (without the signer knowing the content of m). In order to achieve that, the user will generate a coupe of random values \(a, b \in \mathbb{Z}_n\), and from these parameters will compute the blinding factor \(R=aR' + bG = (ak + b)G\), and as \(R\) is a point we can get \(R = (x, y)\). The user can blind the message by computing \(m' = a^{-1} \cdot x \cdot h(m)\), where \(h(m)\) is the hash of the message.
Then, the user sends the blinded message (\(m'\)) to the signer, who will perform the blind signature by computing \(s' = d m' + k\), which is sent back to the user.
The user can unblind the signature by \(s = a s' + b\), and the complete signature will be \((R, s)\).
And now, we are in a point where the signature can be verified by a third party for the signer’s public key by checking \(sG == R + x h(m) Q\).
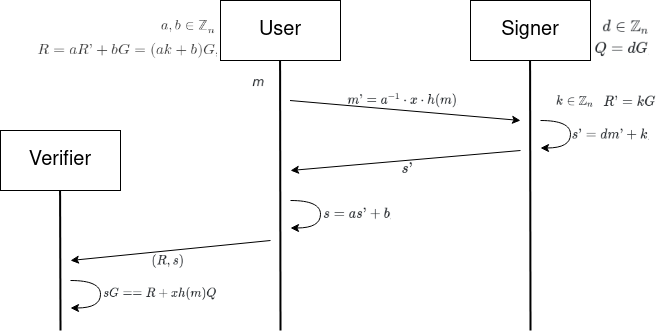 The previous diagram but with the operations from each step.
The previous diagram but with the operations from each step.
From the verification \(sG == R + x h(m) Q\), we can unroll it and check that:
\[ \fbox{sG} = (a s' + b) G = (a (d m' + k) + b) G\newline = (a d m' + ak + b) G = ((a d (a^{-1} x h(m))) + ak + b) G\newline = (d x h(m) + ak + b) G\newline = dG x h(m) + (ak + b)G = \fbox{R + x h(m) Q} \]
Code
Here is an example of how this scheme on the secp256k1 curve could be used using the implementation from go-blindsecp256k1.
import (
[...]
"github.com/arnaucube/go-blindsecp256k1"
)
func main() {
// signer: create new signer key pair
sk := blindsecp256k1.NewPrivateKey()
signerPubK := sk.Public()
// signer: when user requests new R parameter to blind a new msg,
// create new signerR (public) with its secret k
k, signerR := blindsecp256k1.NewRequestParameters()
// user: blinds the msg using signer's R
msg := new(big.Int).SetBytes([]byte("test"))
msgBlinded, userSecretData, err := blindsecp256k1.Blind(msg, signerR)
if err != nil {
panic(err)
}
// signer: signs the blinded message using its private key & secret k
sBlind, err := sk.BlindSign(msgBlinded, k)
if err != nil {
panic(err)
}
// user: unblinds the blinded signature
sig := blindsecp256k1.Unblind(sBlind, userSecretData)
// signature can be verified with signer PublicKey
verified := blindsecp256k1.Verify(msg, sig, signerPubK)
if !verified {
fmt.Println("verification failed")
} else {
fmt.Println("blind signature verified")
}
}
Conclusions
Blind signatures are an interesting concept, which can be used in some use cases specially on voting systems. As we’ve seen, the math background behind it’s not quite complex compared for example to zkSNARKs, and it does not require trusted setups. Although, for most of the cases zkSNARKs have more flexibility, and we could cover similar use cases by proving that the user knows some private key for which the corresponding public key is placed in a leaf of a Merkle Tree for a certain Merkle Root (but this would be out of scope for the current notes).
An implementation of this scheme in Go can be found in: https://github.com/arnaucube/go-blindsecp256k1 (and a compatible Typescript implementation blindsecp256k1-js). A next iteration could be to abstract the curve & keys structures, to use the generic Go ones, so other curves and already existing keys could be used with the same code.
Special thanks to @dhole for reviewing this text.