# Shamir's Secret Sharing

<img src="https://arnaucube.com/img/logoArnauCubeTransparent.png" style="max-width:20%; float:right;" />

- https://arnaucube.com
- https://github.com/arnaucube
- https://twitter.com/arnaucube
<br><br><br>
<div style="float:right;font-size:80%;">
  <a href="https://creativecommons.org/licenses/by-nc-sa/4.0/"><img src="https://licensebuttons.net/l/by-nc-sa/4.0/88x31.png" /></a>
  <br>
  2019-07-05
</div>

---

# Intro
- I'm not an expert on the field, neither a mathematician. Just an engineer with interest for cryptography
- Short talk (15 min), with the objective to make a practical introduction to the Shamir's Secret Sharing algorithm
- Is not a talk about mathematical demostrations, is a talk with the objective to get the basic notions to be able to do a practical implementation of the algorithm
- After the talk, we will do a practical workshop to implement the concepts. We can offer support for Go, Rust, Python and Nodejs (you can choose any other language, but we will not be able to help)

---

- Cryptographic algorithm
- Created by Adi Shamir, in 1979
	- also known by the $RSA$ cryptosystem
		- explained in few months ago in a similar talk: https://github.com/arnaucube/slides/rsa

---
## What's this about?
- imagine having a password that you want to share with 5 persons, in a way that they need to join their parts to get the original password
- take the password, split it in 5 parts, and give one part to each one
- when they need to recover it, they just need to get together, put all the pieces and recover the password (the `secret`)
- this, has the problem that if a person looses its part, the secret will not be recovered anymore.. luckly we have a solution here:

---

- Shamir's Secret Sharing:
	- from a secret to be shared, we generate 5 parts, but we can specify a number of parts that are needed to recover the secret
	- so for example, we generate 5 parts, where we will need only 3 of that 5 parts to recover the secret, and the order doesn't matter
	- we have the ability to define the thresholds of $M$ parts to be created, and $N$ parts to be able the recover

---

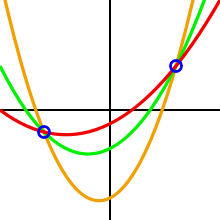
- 2 points are sufficient to define a line
- 3 points are sufficient to define a parabola
- 4 points are sufficient to define a cubic curve
- $K$ points are suficient to define a polynomial of degree $k-1$

We can create infinity of polynomials of degree 2, that goes through 2 points, but with 3 points, we can define a polynomial of degree 2 unique.

![](https://upload.wikimedia.org/wikipedia/commons/thumb/6/66/3_polynomials_of_degree_2_through_2_points.svg/220px-3_polynomials_of_degree_2_through_2_points.svg.png)

---

## Naming

- `s`: secret
- `m`: number of parts to be created
- `n`: number of minimum parts necessary to recover the secret
- `p`: random prime number, the Finite Field will be over that value

---

## Secret generation
- we want that are necessary $n$ parts of $m$ to recover $s$
	- where $n<m$
- need to create a polynomial of degree $n-1$
$f(x) = \alpha_0 + \alpha_1 x  + \alpha_2 x^2 + \alpha_3 x^3 + ... + + \alpha_{n-1} x^{n-1}$
- where $\alpha_0$ is the secret $s$
- $\alpha_i$ are random values that build the polynomial
*where $\alpha_0$ is the secret to share, and $\alpha_i$ are the random values inside the $Finite Field$

---

$f(x) = \alpha_0 + \alpha_1 x  + \alpha_2 x^2 + \alpha_3 x^3 + ... + + \alpha_{n-1} x^{n-1}$

- the packets that we will generate are $P = (x, f(x))$
    - where $x$ is each one of the values between $1$ and $m$
        - $P_1=(1, f(1))$
        - $P_2=(2, f(2))$
        - $P_3=(3, f(3))$
        - ...
        - $P_m=(m, f(m))$

---
## Secret recovery
- in order to recover the secret $s$, we will need a minimum of $n$ points of the polynomial
	- the order doesn't matter
- with that $n$ parts, we do Lagrange Interpolation/Polynomial Interpolation

---

## Polynomial Interpolation / Lagrange Interpolation
- for a group of points, we can find the smallest degree polynomial that goees through all that points
	- this polynomial is unique for each group of points

![](https://upload.wikimedia.org/wikipedia/commons/thumb/5/5a/Lagrange_polynomial.svg/440px-Lagrange_polynomial.svg.png)

---

![](https://www.researchgate.net/profile/Chinthanie_Weerakoon/publication/319703488/figure/fig4/AS:614100010799117@1523424260513/Lagrange-Interpolation-Technique.png)

---

$L(x) = \sum_{j=0}^{n} y_j l_j(x)$

<br><br>

![](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e2c3a2ab16a8723c0446de6a30da839198fb04b)

---

## Wikipedia example
*example over real numbers, in the practical world, we use the algorithm in the Finite Field over $p$
<span style="font-size:70%;float:right;">(more details: https://en.wikipedia.org/wiki/Shamir's_Secret_Sharing#Problem)</span><br>
- $s=1234$
- $m=6$
- $n=3$
- $f(x) = \alpha_0 + \alpha_1 x  + \alpha_2 x^2$
    - $\alpha_0 = s = 1234$
    - $\alpha_1 = 166$ *(random)*
    - $\alpha_2 = 94$ *(random)*
- $f(x) = 1234 + 166 x  + 94 x^2$

---

- $f(x) = 1234 + 166 x  + 94 x^2$
- we calculate the points $P = (x, f(x))$
    - where $x$ is each one of the values between $1$ and $m$
        - $P_1=(1, f(1)) = (1, 1494)$
        - $P_2=(2, f(2)) = (2, 1942)$
        - $P_3=(3, f(3)) = (3, 2578)$
        - $P_4=(4, f(4)) = (4, 3402)$
        - $P_5=(5, f(5)) = (5, 4414)$
        - $P_6=(6, f(6)) = (6, 5614)$
---

- to recover the secret, let's imagine that we take the packets 2, 4, 5
    - $(x_0, y_0) = (2, 1942)$
    - $(x_0, y_0) = (4, 3402)$
    - $(x_0, y_0) = (5, 4414)$

---

- let's calculate the Lagrange Interpolation
    - ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/388471f79b8d3bdb75851b99ed15e5849329cc84)
    - ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c853bdf0daa2db92cd70a6ab21dfd858296cfdd)
    - ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/2013ee56aba68b07d8d4a2c6578e77ff8e8940ff)
    - ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/32fc145272d82d9ebf62b4e30a05eac2b7d2873a)
- obtaining $f(x) = \alpha_0 + \alpha_1 x  + \alpha_2 x^2$, where $\alpha_0$ is the secret $s$ recovered
	- where we eavluate the polynomial at $f(0)$, obtaining $\alpha_0 = s$
- *we are not going into details now, but if you want in the practical workshop we can analyze the 'mathematical' part of all of this

---

# And now... practical implementation
- full night long
- big ints are your friends
- $L(x) = \sum_{j=0}^{n} y_j l_j(x)$
![](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e2c3a2ab16a8723c0446de6a30da839198fb04b)

# About

<img src="https://arnaucube.com/img/logoArnauCubeTransparent.png" style="max-width:20%; float:right;" />

- https://arnaucube.com
- https://github.com/arnaucube
- https://twitter.com/arnaucube
<br>
<div style="float:right;font-size:80%;">
  <a href="https://creativecommons.org/licenses/by-nc-sa/4.0/"><img src="https://licensebuttons.net/l/by-nc-sa/4.0/88x31.png" /></a>
  <br>
  2019-07-05
</div>