arnaucube
/
slides
mirror of https://github.com/arnaucube/slides.git
1
0
Fork 0
Code Issues Projects Releases Wiki Activity
You can not select more than 25 topics Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
2 Commits
1 Branch
0 Tags
2.7 MiB
 
Tree: df47c73acd
Branches Tags
${ item.name }
Create branch ${ searchTerm }
from 'df47c73acd'
${ noResults }
slides/src/zksnarks-from-scratch-a-tec.../zksnarks-from-scratch-a-tec...

23 KiB
Raw Blame History

zkSNARKs from scratch, a technical explanation





iden3.io github.com/iden3 twitter.com/identhree

Warning

  • I'm not a mathematician, this talk is not for mathematicians

  • In free time, have been studying zkSNARKS & implementing it in Go

  • Talk about a technical explaination from an engineer point of view

  • The idea is to try to transmit the learnings from long night study hours during last winter

  • Also at the end will briefly overview how we use zkSNARKs in iden3

  • This slides will be combined with

  • Don't use your own crypto. But it's fun to implement it (only for learning purposes)

Contents

  • Introduction
    • zkSNARK overview
    • zkSNARK flow
    • Generating and verifying proofs
  • Foundations
    • Basics of modular arithmetic
    • Groups
    • Finite fields
    • Elliptic curve operations
  • Pairings
    • Bilinear Pairings
    • BLS signatures
  • zkSNARK (Pinocchio)
    • Circuit compiler
    • R1CS
    • QAP
    • Lagrange Interpolation
    • Trusted Setup
    • Proofs generation
    • Proofs verification
  • Groth16
  • How we use zkSNARKs in iden3
  • libraries
  • Circuit languages
  • utilities (Elliptic curve & Hash functions) inside the zkSNARK libraries
    • BabyJubJub
    • Mimc
    • Poseidon
  • References

Introduction

zkSNARK overview

  • protocol to prove the correctness of a computation
  • useful for
    • scalability
    • privacy
    • interoperability
  • examples:
    • Alice can prove to Brenna that knows $x$ such as $f(x) = y$
    • Brenna can prove to Alice that knows a certain input which $Hash$ results in a certain known value
    • Carol can proof that is a member of an organization without revealing their identity
    • etc

zkSNARK flow

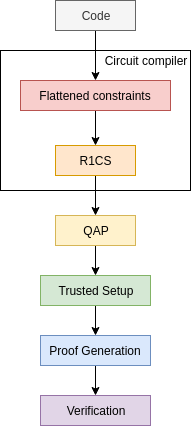
Generating and verifying proofs

Generating a proof:



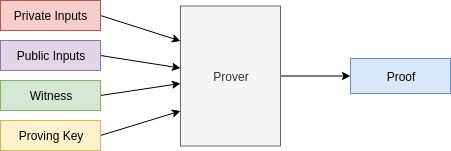
Verifying a proof:

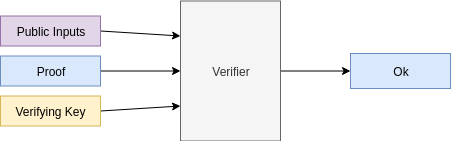
Foundations

  • Modular aritmetic
  • Groups
  • Finite fields
  • Elliptic Curve Cryptography

Basics of modular arithmetic

  • Modulus, mod, %
  • Remainder after division of two numbers

clocks

5 mod 12 = 5
14 mod 12 = 2
83 mod 10 = 3

5 + 3 mod 6 = 8 mod 6 = 2

Groups

  • a set with an operation
    • operation must be associative
  • neutral element ($identity$): adding the neutral element to any element gives the element
  • inverse: $e$ + $e_{inverse}$ = $identity$
  • cyclic groups
    • finite group with a generator element
    • any element must be writable by a multiple of the generator element
  • abelian group
    • group with commutative operation

Finite fields

Elliptic curve

  • point addition

$(x_1, y_1) + (x_2, y_2) = (\dfrac{ x_1 y_2 + x_2 y_1 }{ 1 + d x_1 x_2 y_1 y_2 }, \dfrac{ y_1 y_2 - x_1 x_2 }{ 1-dx_1 x_2 y_1 y_2 })$

  • G1
  • G2

(whiteboard explanation)

Pairings

  • 3 typical types used for SNARKS:
    • BN (Barreto Naehrig) - used in Ethereum
    • BLS (Barreto Lynn Scott) - used in ZCash & Ethereum 2.0
    • MNT (Miyaji- Nakabayashi - Takano) - used in CodaProtocol
  • $y^2 = x^3 + b$ with embedding degree 12
  • function that maps (pairs) two points from sets S1 and S2 into another set S3
  • is a bilinear function
  • $e(G_1, G_2) -> G_T$
  • the groups must be
    • cyclic
    • same prime order ($r$)
  • $F_q$, where $q=$21888242871839275222246405745257275088696311157297823662689037894645226208583
  • $F_r$, where $r=$21888242871839275222246405745257275088548364400416034343698204186575808495617

Bilinear Pairings

$e(P_1 + P_2, Q_1) == e(P_1, Q_1) \cdot e(P_2, Q_1)$

$e(P_1, Q_1 + Q_2) == e(P_1, Q_1) \cdot e(P_1, Q_2)$

$e(aP, bQ) == e(P, Q)^{ab} == e(bP, aQ)$

$e(g_1, g_2)^6 == e(g_1, 6 \cdot g_2)$

$e(g_1, g_2)^6 == e(6 \cdot g_1, g_2)$

$e(g_1, g_2)^6 == e(3 \cdot g_1, 2 g_2)$

$e(g_1, g_2)^6 == e(2 \cdot g_1, 3 g_2)$

BLS signatures

(small overview, is offtopic here, but is interesting)

  • key generation
    • random private key $x$ in $[0, r-1]$
    • public key $g^x$
  • signature
    • $h=Hash(m)$ (over G2)
    • signature $\sigma=h^x$
  • verification
    • check that: $e(g, \sigma) == e(g^x, Hash(m))$ $e(g, h^x) == e(g^x, h)$
  • aggregate signatures
    • $s = s0 + s1 + s2 ...$
  • verify aggregated signatures

$e(G,S) == e(P, H(m))$

$e(G, s0+s1+s2...) == e(p0, H(m)) \cdot e(p1, H(m)) \cdot e(p2, H(m)) ...$

More info: https://crypto.stanford.edu/~dabo/pubs/papers/BLSmultisig.html

Circuit compiler

  • not a software compiler -> a constraint prover

    • what this means

  • constraint concept

    • value0 == value1 <operation> value2

  • want to proof that a certain computation has been done correctly

  • graphic of circuit with gates (whiteboard)

  • about high level programing languages for zkSNARKS, by Harry Roberts: https://www.youtube.com/watch?v=nKrBJo3E3FY

Circuit code example: $f(x) = x^5 + 2\cdot x + 6$

func exp5(private a):
	b = a * a
	c = a * b
	d = a * c
	e = a * d
	return e

func main(private s0, public s1):
	s2 = exp5(s0)
	s3 = s0 * 2
	s4 = s3 + s2
	s5 = s4 + 6
	equals(s1, s5)
	out = 1 * 1

Inputs and Witness

For a certain circuit, with the inputs that we calculate the Witness for the circuit signals

  • private inputs: [8]
    • in this case the private input is the 'secret' $x$ value that computed into the equation gives the expected $f(x)$
  • public inputs: [32790]
    • in this case the public input is the result of the equation
  • signals: [one s1 s0 b0 c0 d0 s2 s3 s4 s5 out]
  • witness: [1 32790 8 64 512 4096 32768 16 32784 32790 1]

R1CS

  • Rank 1 Constraint System
  • way to write down the constraints by 3 linear combinations
  • 1 constraint per operation
  • $(A, B, C) = A.s \cdot B.s - C.s = 0$
  • from flat code constraints we can generate the R1CS

R1CS

$(a_{11}s_1 + a_{12}s_2 + ... + a_{1n}s_n) \cdot (b_{11}s_1 + b_{12}s_2 + ... + b_{1n}s_n) - (c_{11}s_1 + c_{12}s_2 + ... + c_{1n}s_n) = 0$

$(a_{21}s_1 + a_{22}s_2 + ... + a_{2n}s_n) \cdot (b_{21}s_1 + b_{22}s_2 + ... + b_{2n}s_n) - (c_{21}s_1 + c_{22}s_2 + ... + c_{2n}s_n) = 0$ $(a_{31}s_1 + a_{32}s_2 + ... + a_{3n}s_n) \cdot (b_{31}s_1 + b_{32}s_2 + ... + b_{3n}s_n) - (c_{31}s_1 + c_{32}s_2 + ... + c_{3n}s_n) = 0$ [...] $(a_{m1}s_1 + a_{m2}s_2 + ... + a_{mn}s_n) \cdot (b_{m1}s_1 + b_{m2}s_2 + ... + b_{mn}s_n) - (c_{m1}s_1 + c_{m2}s_2 + ... + c_{mn}s_n) = 0$

*where $s$ are the signals of the circuit, and we need to find $a, b, c$ that satisfies the equations

R1CS constraint example:

  • signals: [one s1 s0 b0 c0 d0 s2 s3 s4 s5 out]
  • witness: [1 32790 8 64 512 4096 32768 16 32784 32790 1]
  • First constraint flat code: b0 == s0 * s0
  • R1CS first constraint: $A_1 = [00100000000]$ $B_1 = [00100000000]$ $C_1 = [00010000000]$

R1CS example:

$A$ $B$ $C$:
$[0 0 1 0 0 0 0 0 0 0 0]$
$[0 0 1 0 0 0 0 0 0 0 0]$
$[0 0 1 0 0 0 0 0 0 0 0]$
$[0 0 1 0 0 0 0 0 0 0 0]$
$[0 0 1 0 0 0 0 0 0 0 0]$
$[0 0 0 0 0 0 1 1 0 0 0]$
$[6 0 0 0 0 0 0 0 1 0 0]$
$[0 0 0 0 0 0 0 0 0 1 0]$
$[0 1 0 0 0 0 0 0 0 0 0]$
$[1 0 0 0 0 0 0 0 0 0 0]$		 $[0 0 1 0 0 0 0 0 0 0 0]$
$[0 0 0 1 0 0 0 0 0 0 0]$
$[0 0 0 0 1 0 0 0 0 0 0]$
$[0 0 0 0 0 1 0 0 0 0 0]$
$[2 0 0 0 0 0 0 0 0 0 0]$
$[1 0 0 0 0 0 0 0 0 0 0]$
$[1 0 0 0 0 0 0 0 0 0 0]$
$[1 0 0 0 0 0 0 0 0 0 0]$
$[1 0 0 0 0 0 0 0 0 0 0]$
$[1 0 0 0 0 0 0 0 0 0 0]$		 $[0 0 0 1 0 0 0 0 0 0 0]$
$[0 0 0 0 1 0 0 0 0 0 0]$
$[0 0 0 0 0 1 0 0 0 0 0]$
$[0 0 0 0 0 0 1 0 0 0 0]$
$[0 0 0 0 0 0 0 1 0 0 0]$
$[0 0 0 0 0 0 0 0 1 0 0]$
$[0 0 0 0 0 0 0 0 0 1 0]$
$[0 1 0 0 0 0 0 0 0 0 0]$
$[0 0 0 0 0 0 0 0 0 1 0]$
$[0 0 0 0 0 0 0 0 0 0 1]$

QAP

qap

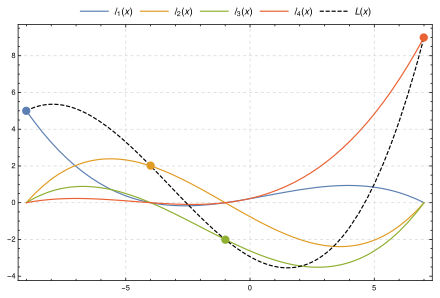
Lagrange Interpolation

(Polynomial Interpolation)

  • for a group of points, we can find the smallest degree polynomial that goees through all that points
    • this polynomial is unique for each group of points

$L(x) = \sum_{j=0}^{n} y_j l_j(x)$



Shamir's Secret Sharing

(small overview, is offtopic here, but is interesting)

  • from a secret to be shared, we generate 5 parts, but we can specify a number of parts that are needed to recover the secret
  • so for example, we generate 5 parts, where we will need only 3 of that 5 parts to recover the secret, and the order doesn't matter
  • we have the ability to define the thresholds of $M$ parts to be created, and $N$ parts to be able the recover
Shamir's Secret Sharing - Secret generation
  • we want that are necessary $n$ parts of $m$ to recover $s$
    • where $n<m$
  • need to create a polynomial of degree $n-1$ $f(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2 + \alpha_3 x^3 + ... + + \alpha_{n-1} x^{n-1}$
  • where $\alpha_0$ is the secret $s$
  • $\alpha_i$ are random values that build the polynomial *where $\alpha_0$ is the secret to share, and $\alpha_i$ are the random values inside the $Finite Field$

$f(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2 + \alpha_3 x^3 + ... + + \alpha_{n-1} x^{n-1}$

  • the packets that we will generate are $P = (x, f(x))$
    • where $x$ is each one of the values between $1$ and $m$
      • $P_1=(1, f(1))$
      • $P_2=(2, f(2))$
      • $P_3=(3, f(3))$
      • ...
      • $P_m=(m, f(m))$
Shamir's Secret Sharing - Secret recovery
  • in order to recover the secret $s$, we will need a minimum of $n$ points of the polynomial
    • the order doesn't matter
  • with that $n$ parts, we do Lagrange Interpolation/Polynomial Interpolation, recovering the original polynomial

QAP

$(\alpha_1(x)s_1 + \alpha_2(x)s_2 + ... + \alpha_n(x)s_n) \cdot (\beta_1(x)s_1 + \beta_2(x)s_2 + ... + \beta_n(x)s_n) - (\gamma_1(x)s_1 + \gamma_2(x)s_2 + ... + \gamma_n(x)s_n) = P(x)$

|----------------------- $A(x)$ -----------------------|------------------------ $B(x)$ -----------------------|------------------------ $C(x)$ ------------------------|

  • $P(x) = A(x)B(x)-C(x)$
  • $P(x) = Z(x) h(x)$
  • $Z(x)$: divisor polynomial
    • $Z(x) = (x - x_1)(x-x_2)...(x-x_m) => ...=> (x_1, 0), (x_2, 0), ..., (x_m, 0)$
      • optimizations with FFT
  • $h(x) = P(x) / Z(x)$

The following explanation is for the Pinocchio protocol, all the examples will be for this protocol. The Groth16 is explained also in the end of this slides.

Trusted Setup

  • concept
  • $\tau$ (Tau)
  • "Toxic waste"
  • Proving Key
  • Verification Key

$g_1 t^0, g_1 t^1, g_1 t^2, g_1 t^3, g_1 t^4, ...$ $g_2 t^0, g_2 t^1, g_2 t^2, g_2 t^3, g_2 t^4, ...$

Proving Key: $pk = (C, pk_A, pk_A', pk_B, pk_B', pk_C, pk_C', pk_H)$ where:

  • $pk_A = { A_i(\tau) \rho_A P_1 }^{m+3}_{i=0}$
  • $pk_A' = { A_i(\tau) \alpha_A \rho_A P_1 }^{m+3}_{i=n+1}$
  • $pk_B = { B_i(\tau) \rho_B P_2 }^{m+3}_{i=0}$
  • $pk_B' = { B_i(\tau) \alpha_B \rho_B P_1 }^{m+3}_{i=0}$
  • $pk_C = { C_i(\tau) \rho_C P_1 }^{m+3}{i=0} = {C_i(\tau) \rho_A \rho_B P_1}^{m+3}{i=0}$
  • $pk_C' = { C_i(\tau) \alpha_C \rho_C P_1 }^{m+3}{i=0} = { C_i(\tau) \alpha_C \rho_A \rho_B P_1 }^{m+3}{i=0}$
  • $pk_K = { \beta (A_i(\tau) \rho_A + B_i(\tau) \rho_B C_i(\tau) \rho_A \rho_B) P_1 } ^{m+3}_{i=0}$
  • $pk_H = { \tau^i P_1 }^d_{i=0}$

where:

  • $d$: degree of polynomial $Z(x)$
  • $m$: number of circuit signals

Verification Key: $vk = (vk_A, vk_B, vk_C, vk_\gamma, vk^1_{\beta\gamma}, vk^2_{\beta\gamma}, vk_Z, vk_{IC})$

  • $vk_A = \alpha_A P_2$, $vk_B = \alpha_B P_1$, $vk_C = \alpha_C P_2$
  • $vk_{\beta\gamma} = \gamma P_2$, $vk^1_{\beta\gamma} = \beta\gamma P_1$, $vk^2_{\beta\gamma} = \beta\gamma P_2$
  • $vk_Z = Z(\tau) \rho_A \rho_B P_2$, $vk_{IC} = (A_i(\tau) \rho_A P_1)^n_{i=0}$
type Pk struct { // Proving Key pk:=(pkA, pkB, pkC, pkH)
        G1T [][3]*big.Int // t encrypted in G1 curve, G1T == Pk.H
        A   [][3]*big.Int
        B   [][3][2]*big.Int
        C   [][3]*big.Int
        Kp  [][3]*big.Int
        Ap  [][3]*big.Int
        Bp  [][3]*big.Int
        Cp  [][3]*big.Int
        Z   []*big.Int
}

type Vk struct {
        Vka   [3][2]*big.Int
        Vkb   [3]*big.Int
        Vkc   [3][2]*big.Int
        IC    [][3]*big.Int
        G1Kbg [3]*big.Int    // g1 * Kbeta * Kgamma
        G2Kbg [3][2]*big.Int // g2 * Kbeta * Kgamma
        G2Kg  [3][2]*big.Int // g2 * Kgamma
        Vkz   [3][2]*big.Int
}

// Setup is the data structure holding the Trusted Setup data. The Setup.Toxic sub struct must be destroyed after the GenerateTrustedSetup function is completed
type Setup struct {
        Toxic struct {
                T      *big.Int // trusted setup secret
                Ka     *big.Int
                Kb     *big.Int
                Kc     *big.Int
                Kbeta  *big.Int
                Kgamma *big.Int
                RhoA   *big.Int
                RhoB   *big.Int
                RhoC   *big.Int
        }
        Pk Pk
        Vk Vk
}

Proofs generation

  • $A, B, C, Z$ (from the QAP)
  • random $\delta_1, \delta_2, \delta_3$
  • $H(z)= \dfrac{A(z)B(z)-C(z)}{Z(z)}$
    • $A(z) = A_0(z) + \sum_{i=1}^m s_i A_i(x) + \delta_1 Z(z)$
    • $B(z) = B_0(z) + \sum_{i=1}^m s_i B_i(x) + \delta_2 Z(z)$
    • $C(z) = C_0(z) + \sum_{i=1}^m s_i B_i(x) + \delta_2 Z(z)$ (where $m$ is the number of public inputs)
  • $\pi_A = <c, pk_A>$
  • $\pi_A' = <c, pk_A'>$
  • $\pi_B = <c, pk_B>$
    • example:
    for i := 0; i < circuit.NVars; i++ {
    proof.PiB = Utils.Bn.G2.Add(proof.PiB, Utils.Bn.G2.MulScalar(pk.B[i], w[i]))
    proof.PiBp = Utils.Bn.G1.Add(proof.PiBp, Utils.Bn.G1.MulScalar(pk.Bp[i], w[i]))
}

($c=1+witness+\delta_1+\delta_2+\delta_3$

  • $\pi_B' = <c, pk_B'>$
  • $\pi_C = <c, pk_C>$
  • $\pi_C' = <c, pk_C'>$
  • $\pi_K = <c, pk_K>$
  • $\pi_H = <h, pk_KH>$
  • proof: $\pi = (\pi_A, \pi_A', \pi_B, \pi_B', \pi_C, \pi_C', \pi_K, \pi_H$

Proofs verification

  • $vk_{kx} = vk_{IC,0} + \sum_{i=1}^n x_i vk_{IC,i}$

Verification:

  • $e(\pi_A, vk_a) == e(\pi_{A'}, g_2)$
  • $e(vk_b, \pi_B) == e(\pi_{B'}, g_2)$
  • $e(\pi_C, vk_c) == e(\pi_{C'}, g_2)$
  • $e(vk_{kx}+\pi_A, \pi_B) == e(\pi_H, vk_{kz}) \cdot e(\pi_C, g_2)$
  • $e(vk_{kx} + \pi_A + \pi_C, V_{\beta\gamma}^2) \cdot e(vk_{\beta\gamma}^1, \pi_B) == e(\pi_k, vk_{\gamma}^1)$
Example (whiteboard):

$\dfrac{ e(\pi_A, \pi_B) }{ e(\pi_C, g_2) } = e(g_1 h(t), g_2 z(t)) $
$\dfrac{ e(A_1 + A_2 + ... + A_n, B_1 + B_2 + ... + B_n) }{ e(C_1 + C_2 + ... + C_n, g_2) } = e(g_1 h(t), g_2 z(t)) $
$\dfrac{ e(g_1 \alpha_1(t) s_1 + g_1 \alpha_2(t) s_2 + ... + g_1 \alpha_n(t) s_n, g_2 \beta_1(t)s_1 + g_2 \beta_2(t) s_2 + ... + g_2 \beta_n(t) s_n) }{ e(g_1 \gamma_1(t) s_1 + g_1 \gamma_2(t) s_2 + ... + g_1 \gamma_n(t) s_n, g_2) } = e(g_1 h(t), g_2 z(t)) $
$ e(g_1 \alpha_1(t) s_1 + g_1 \alpha_2(t) s_2 + ... + g_1 \alpha_n(t) s_n, g_2 \beta_1(t)s_1 + g_2 \beta_2(t) s_2 + ... + g_2 \beta_n(t) s_n)$ $= e(g_1 h(t), g_2 z(t)) \cdot e(g_1 \gamma_1(t) s_1 + g_1 \gamma_2(t) s_2 + ... + g_1 \gamma_n(t) s_n, g_2) $

Groth16

Trusted Setup

$\tau = \alpha, \beta, \gamma, \delta, x$

$\sigma_1 =$

  • $\alpha, \beta, \delta, { x^i}_{i=0}^{n-1}$

  • ${ \dfrac{ \beta u_i(x) + \alpha v_i(x) + w_i(x) }{ \gamma } }_{i=0}^l$

  • ${ \dfrac{ \beta u_i(x) + \alpha v_i(x) + w_i(x) }{ \delta } }_{i=l+1}^m$

  • ${ \dfrac{x^i t(x)}{\delta} }_{i=0}^{n-2}$

$\sigma_2 = (\beta, \gamma, \delta, { x^i }_{i=0}^{n-1})$

(where $u_i(x), v_i(x), w_i(x)$ are the $QAP$)

type Pk struct { // Proving Key
	BACDelta [][3]*big.Int // {( βui(x)+αvi(x)+wi(x) ) / δ } from l+1 to m
	Z        []*big.Int
	G1       struct {
		Alpha    [3]*big.Int
		Beta     [3]*big.Int
		Delta    [3]*big.Int
		At       [][3]*big.Int // {a(τ)} from 0 to m
		BACGamma [][3]*big.Int // {( βui(x)+αvi(x)+wi(x) ) / γ } from 0 to m
	}
	G2 struct {
		Beta     [3][2]*big.Int
		Gamma    [3][2]*big.Int
		Delta    [3][2]*big.Int
		BACGamma [][3][2]*big.Int // {( βui(x)+αvi(x)+wi(x) ) / γ } from 0 to m
	}
	PowersTauDelta [][3]*big.Int // powers of τ encrypted in G1 curve, divided by δ
}

type Vk struct {
	IC [][3]*big.Int
	G1 struct {
		Alpha [3]*big.Int
	}
	G2 struct {
		Beta  [3][2]*big.Int
		Gamma [3][2]*big.Int
		Delta [3][2]*big.Int
	}
}

// Setup is the data structure holding the Trusted Setup data. The Setup.Toxic sub struct must be destroyed after the GenerateTrustedSetup function is completed
type Setup struct {
	Toxic struct {
		T      *big.Int // trusted setup secret
		Kalpha *big.Int
		Kbeta  *big.Int
		Kgamma *big.Int
		Kdelta *big.Int
	}
	Pk Pk
	Vk Vk
}

Proofs Generation

$\pi_A=\alpha + \sum_{i=0}^m \alpha_i u_i(x) + r \delta$ $\pi_B=\beta + \sum_{i=0}^m \alpha_i v_i(x) + s \delta$

$\pi_C = \dfrac{ \sum_{i=l+1}^m a_i(\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x)t(x) }{ \delta } + \pi_As + \pi_Br -rs\delta$

$\pi=\pi_A^1, \pi_B^1, \pi_C^2$

Proof Verification

$[\pi_A]_1 \cdot [\pi_B]_2 = [\alpha]_1 \cdot [\beta]2 + \sum{i=0}^l a_i [ \dfrac{ \beta u_i(x) + \alpha v_i(x) + w_i(x) }{ \gamma } ]_1 \cdot [\gamma]_2 + [\pi_C]_1 \cdot [\delta]_2 $

$e(\pi_A, \pi_B) = e(\alpha, \beta) \cdot e(pub, \gamma) \cdot e(\pi_C, \delta)$

How we use zkSNARKs in iden3

  • proving a credentials without revealing it's content
  • proving that an identity has a claim issued by another identity, without revealing all the data
  • proving any property of an identity
  • $ITF$ (Identity Transition Function), a way to prove with a zkSNARK that an identity has been updated following the defined protocol
    • identities can not cheat when issuing claims
  • etc

Other ideas for free time side project

  • Zendermint (Tendermint + zkSNARKs)

zkSNARK libraries

Circuit languages

language snark library with which plugs in
Zokrates libsnark, bellman
Snarky libsnark
circom snarkjs, websnark, bellman
go-snark-circuit go-snark

Utilities (Elliptic curve & Hash functions) inside the zkSNARK

  • we work over $F_r$, where $r=$21888242871839275222246405745257275088548364400416034343698204186575808495617

  • BabyJubJub

  • Mimc

  • Poseidon

Utilities (Elliptic curve & Hash functions) inside the zkSNARK

BabyJubJub

Utilities (Elliptic curve & Hash functions) inside the zkSNARK

Mimc7

Utilities (Elliptic curve & Hash functions) inside the zkSNARK

Poseidon

References

Thank you very much


iden3.io github.com/iden3 twitter.com/identhree