first commit, add slides: zksnarks, shamirsecretsharing, rsa
7
README.md
Normal file
@@ -0,0 +1,7 @@
|
||||
# slides
|
||||
|
||||
- [RSA and Homomorphic Multiplication](https://github.com/arnaucube/slides/blob/master/rsa-and-homomorphicmultiplication.pdf)
|
||||
- [Shamir's Secret Sharing](https://github.com/arnaucube/slides/blob/master/rsa-and-homomorphicmultiplication.pdf)
|
||||
- [zkSNARKs from scratch, a technical explanation](https://github.com/arnaucube/slides/blob/master/zksnarks-from-scratch-a-technical-explanation.pdf)
|
||||
|
||||
Any error, typo, mistake, etc, open an issue or a pull request and I'll be glad to fix it.
|
||||
BIN
rsa-and-homomorphicmultiplication.pdf
Normal file
BIN
shamirsecretsharing.pdf
Normal file
@@ -0,0 +1,358 @@
|
||||
# RSA and Homomorphic Multiplication
|
||||
|
||||
<img src="https://arnaucube.com/img/logoArnauCubeTransparent.png" style="max-width:20%; float:right;" />
|
||||
|
||||
|
||||
- https://arnaucube.com
|
||||
- https://github.com/arnaucube
|
||||
- https://twitter.com/arnaucube
|
||||
<br><br><br>
|
||||
<div style="float:right;font-size:80%;">
|
||||
<a href="https://creativecommons.org/licenses/by-nc-sa/4.0/"><img src="https://licensebuttons.net/l/by-nc-sa/4.0/88x31.png" /></a>
|
||||
<br>
|
||||
2018-11-30
|
||||
</div>
|
||||
|
||||
---
|
||||
|
||||
- Intro
|
||||
- Public key cryptography
|
||||
- Basics of modular arithmetic
|
||||
- Brief history of RSA
|
||||
- Keys generation
|
||||
- Prime numbers
|
||||
- Encryption
|
||||
- Decryption
|
||||
- What's going on in encryption and decryption?
|
||||
- Signature
|
||||
- Verification of the signature
|
||||
- Homomorphic Multiplication with RSA
|
||||
- Resources
|
||||
|
||||
---
|
||||
# Intro
|
||||
- I'm not an expert on the field, neither a mathematician. Just an engineer with interest for cryptography
|
||||
- Short talk (15 min), with the objective to make a practical introduction to the RSA cryptosystem
|
||||
- Is not a talk about mathematical demostrations, is a talk with the objective to get the basic notions to be able to do a practical implementation of the algorithm
|
||||
- After the talk, we will do a practical workshop to implement the concepts. We can offer support for Go, Rust, Python and Nodejs (you can choose any other language, but we will not be able to help)
|
||||
|
||||
---
|
||||
# Public key cryptography
|
||||

|
||||
|
||||
---
|
||||
Some examples:
|
||||
- RSA
|
||||
- Paillier
|
||||
- ECC (Corba el·líptica)
|
||||
|
||||
---
|
||||
# Basics of modular arithmetic
|
||||
- Modulus, `mod`, `%`
|
||||
- Remainder after division of two numbers
|
||||
|
||||

|
||||
|
||||
```
|
||||
5 mod 12 = 5
|
||||
14 mod 12 = 2
|
||||
83 mod 10 = 3
|
||||
```
|
||||
|
||||
```
|
||||
5 + 3 mod 6 = 8 mod 6 = 2
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
# Brief history of RSA
|
||||
- RSA (Rivest–Shamir–Adleman): Ron Rivest, Adi Shamir, Leonard Adleman
|
||||
- year 1977
|
||||
- one of the first public key cryptosystems
|
||||
- based on the difficulty of factorization of the product of two big prime numbers
|
||||
|
||||
---
|
||||
# Prime numbers
|
||||
- We need an asymmetric key, in a way where we can decrypt a message encrypted with the asymetric key
|
||||
- Without allowing to find the private key from the public key
|
||||
- in RSA we resolve this with factorization of prime numbers
|
||||
- using prime numbers for $p$ and $q$, it's difficult factorize $n$ to obtain $p$ and $q$, where $n=p*q$
|
||||
|
||||
---
|
||||
|
||||
Example:
|
||||
If we know $n$ which we need to find the $p$ and $q$ values where $p*q=n$:
|
||||
```
|
||||
n = 35
|
||||
```
|
||||
To obtain the possible factors, is needed to brute force trying different combinations, until we find:
|
||||
```
|
||||
p = 5
|
||||
q = 7
|
||||
```
|
||||
In this case is easy as it's a simple example with small numbers. The idea is to do this with big prime numbers
|
||||
|
||||
---
|
||||
|
||||
Another exmample with more bigger prime numbers:
|
||||
```
|
||||
n = 272604817800326282194810623604278579733
|
||||
```
|
||||
From $n$, I don't have a 'direct' way to obtain $p$ and $q$. I need to try by brute force the different values until finding a correct combination.
|
||||
```
|
||||
p = 17975460804519255043
|
||||
q = 15165386899666573831
|
||||
n = 17975460804519255043 * 15165386899666573831 = 272604817800326282194810623604278579733
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
If we do this with non prime numbers:
|
||||
```
|
||||
n = 32
|
||||
We can factorize 32 = 2 * 2 * 2 * 2 * 2
|
||||
combining that values in two values X * Y
|
||||
for example (2*2*2) * (2*2) = 8*4 = 32
|
||||
we can also take 2 * (2*2*2*2) = 2 * 16 = 32
|
||||
...
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
One example with bigger non prime numbers:
|
||||
```
|
||||
n = 272604817800326282227951471308464408608
|
||||
We can take:
|
||||
p = 17975460804519255044
|
||||
q = 15165386899666573832
|
||||
|
||||
Or also:
|
||||
p = 2
|
||||
q = 136302408900163141113975735654232204304
|
||||
...
|
||||
```
|
||||
|
||||
In the real world:
|
||||
- https://en.wikipedia.org/wiki/RSA_numbers
|
||||
- https://en.wikipedia.org/wiki/RSA_Factoring_Challenge#The_prizes_and_records
|
||||
|
||||
So, we are basing this in the fact that is not easy to factorize big numbers composed by big primes.
|
||||
|
||||
|
||||
---
|
||||
# Keys generation
|
||||
- PubK: $e$, $n$
|
||||
- PrivK: $d$, $n$
|
||||
- are choosen randomly 2 big prime numbers $p$ and $q$, that will be secrets
|
||||
- $n = p * q$
|
||||
- $λ$ is the Carmichael function
|
||||
- $λ(n) = (p − 1) * (q − 1)$
|
||||
- Choose a prime number $e$ that satisfies $1 < e < λ(n)$ and $gcd(e, λ(n))=1$
|
||||
- Usually in examples is used $e = 2^16 + 1 = 65537$
|
||||
- $d$ such as $e * d = 1 mod λ(n)$
|
||||
- $d = e^(-1) mod λ(n) = e modinv λ(n)$
|
||||
|
||||
---
|
||||
|
||||
### Example
|
||||
- `p = 3`
|
||||
- `q = 11`
|
||||
- `e = 7` value choosen between 1 and λ(n)=20, where λ(n) is not divisible by this value
|
||||
- `n = 3 * 11 = 33`
|
||||
- `λ(n) = (3-1) * (11-1) = 2 * 10 = 20`
|
||||
- `d` such as `7 * d = 1 mod 20`
|
||||
- `d = 3`
|
||||
- PubK: `e=7, n=33`
|
||||
- PrivK: `d=3, n=33`
|
||||
|
||||
---
|
||||
|
||||
### Naive code
|
||||
```python
|
||||
def egcd(a, b):
|
||||
if a == 0:
|
||||
return (b, 0, 1)
|
||||
g, y, x = egcd(b%a,a)
|
||||
return (g, x - (b//a) * y, y)
|
||||
|
||||
def modinv(a, m):
|
||||
g, x, y = egcd(a, m)
|
||||
if g != 1:
|
||||
raise Exception('No modular inverse')
|
||||
return x%m
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
```
|
||||
def newKeys():
|
||||
p = number.getPrime(n_length)
|
||||
q = number.getPrime(n_length)
|
||||
|
||||
# pubK e, n
|
||||
e = 65537
|
||||
n = p*q
|
||||
pubK = PubK(e, n)
|
||||
|
||||
# privK d, n
|
||||
phi = (p-1) * (q-1)
|
||||
d = modinv(e, phi)
|
||||
privK = PrivK(d, n)
|
||||
|
||||
return({'pubK': pubK, 'privK': privK})
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
# Encryption
|
||||
- Brenna wants to send the message `m` to Alice, so, will use the Public Key from Alice to encrypt `m`
|
||||
- `m` powered at `e` of the public key from Alice
|
||||
- evaluate at modulus of `n`
|
||||
|
||||
### Example
|
||||
- message to encrypt `m = 5`
|
||||
- receiver public key: `e=7, n=33`
|
||||
- `c = 5 ^ 7 mod 33 = 78125 mod 33 = 14`
|
||||
|
||||
### Naive code
|
||||
```python
|
||||
def encrypt(pubK, m):
|
||||
c = (m ** pubK.e) % pubK.n
|
||||
return c
|
||||
```
|
||||
|
||||
---
|
||||
# Decrypt
|
||||
- from an encrypted value `c`
|
||||
- `c` powered at `d` of the private key of the person to who the message was encrypted
|
||||
- evaluate at modulus of `n`
|
||||
|
||||
### Example
|
||||
- receiver private key, PrivK: `d=3, n=33`
|
||||
- `m = 14 ^ 3 mod 33 = 2744 mod 33 = 5`
|
||||
|
||||
### Naive code
|
||||
```python
|
||||
def decrypt(privK, c):
|
||||
m_d = (c ** privK.d) % privK.n
|
||||
return m_d
|
||||
```
|
||||
|
||||
---
|
||||
# What's going on when encrypting and decrypting?
|
||||
|
||||

|
||||
|
||||
---
|
||||
|
||||
```
|
||||
n = pq
|
||||
e
|
||||
phi = (p-1)(q-1)
|
||||
d = e^-1 mod (phi) = e^-1 mod (p-1)(q-1)
|
||||
|
||||
# encrypt
|
||||
c = m^e mod n = m^e mod pq
|
||||
|
||||
# decrypt
|
||||
m' = c^d mod n = c ^(e^-1 mod (p-1)(q-1)) mod pq =
|
||||
= (m^e)^(e^-1 mod (p-1)(q-1)) mod pq =
|
||||
= m^(e * e^-1 mod (p-1)(q-1)) mod pq =
|
||||
= m^(1 mod (p-1)(q-1)) mod pq =
|
||||
[theorem in which we're not going into details]
|
||||
a ^ (1 mod λ(N)) mod N = a mod N
|
||||
[/theorem]
|
||||
= m mod pq
|
||||
```
|
||||
|
||||
|
||||
---
|
||||
# Signature
|
||||
- encryption operation but using PrivK instead of PubK, and PubK instead of PrivK
|
||||
|
||||
- having a message `m`
|
||||
- power of `m` at `d` of the private key from the signer person
|
||||
- evaluated at modulus `n`
|
||||
|
||||
---
|
||||
|
||||
### Example
|
||||
- private key of the person emitter of the signature: `d = 3, n = 33`
|
||||
- message to be signed: `m=5`
|
||||
- signature: `s = 5 ** 3 % 33 = 26`
|
||||
|
||||
### Naive code
|
||||
```python
|
||||
def sign(privK, m):
|
||||
s = (m ** privK.d) % privK.n
|
||||
return s
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
# Verification of the signature
|
||||
- having message `m` and the signature `s`
|
||||
- elevate `m` at `e` of the public key from the signer
|
||||
- evaluate at modulus of `n`
|
||||
|
||||
---
|
||||
|
||||
### Example
|
||||
- public key from the singer person `e=7, n=33`
|
||||
- message `m=5`
|
||||
- signature `s=26`
|
||||
- verification `v = 26**7 % 33 = 5`
|
||||
- check that we have recovered the message (that `m` is equivalent to `v`) `m = 5 = v = 5`
|
||||
|
||||
### Naive code
|
||||
```python
|
||||
def verifySign(pubK, s, m):
|
||||
v = (s ** pubK.e) % privK.n
|
||||
return v==m
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
# Homomorphic Multiplication
|
||||
- from two values $a$ and $b$
|
||||
- encrypted are $a_{encr}$ and $b_{encr}$
|
||||
- we can compute the multiplication of the two encrypted values, obtaining the result encrypted
|
||||
- the encrypted result from the multiplication is calculated doing: $c_{encr} = a_{encr} * b_{encr} mod n$
|
||||
- we can decrypt $c_{encr}$ and we will obtain $c$, equivalent to $a * b$
|
||||
|
||||
- Why:
|
||||
```
|
||||
((a^e mod n) * (b^e mod n)) mod n =
|
||||
= (a^e * b^e mod n) mod n = (a*b)^e mod n
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
### Example
|
||||
- PubK: `e=7, n=33`
|
||||
- PrivK: `d=3, n=33`
|
||||
- `a = 5`
|
||||
- `b = 8`
|
||||
- `a_encr = 5^7 mod 33 = 78125 mod 33 = 14`
|
||||
- `b_encr = 8^7 mod 33 = 2097152 mod 33 = 2`
|
||||
- `c_encr = (14 * 2) mod 33 = 28 mod 33 = 28`
|
||||
- `c = 28 ^ 3 mod 33 = 21952 mod 33 = 7`
|
||||
- `c = 7 = a * b % n = 5 * 8 % 33 = 7`, on `5*8 mod 33 = 7`
|
||||
- take a `n` enough big, if not the result will be cropped by the modulus
|
||||
|
||||
---
|
||||
|
||||
### Naive code
|
||||
```python
|
||||
def homomorphic_mul(pubK, a, b):
|
||||
c = (a*b) % pubK.n
|
||||
return c
|
||||
```
|
||||
|
||||
---
|
||||
# Small demo
|
||||
[...]
|
||||
|
||||
# And now... practical implementation
|
||||
- full night long
|
||||
- big ints are your friends
|
||||
176
src/shamirsecretsharing/shamirsecretsharing.md
Normal file
@@ -0,0 +1,176 @@
|
||||
# Shamir's Secret Sharing
|
||||
|
||||
<img src="https://arnaucube.com/img/logoArnauCubeTransparent.png" style="max-width:20%; float:right;" />
|
||||
|
||||
- https://arnaucube.com
|
||||
- https://github.com/arnaucube
|
||||
- https://twitter.com/arnaucube
|
||||
<br><br><br>
|
||||
<div style="float:right;font-size:80%;">
|
||||
<a href="https://creativecommons.org/licenses/by-nc-sa/4.0/"><img src="https://licensebuttons.net/l/by-nc-sa/4.0/88x31.png" /></a>
|
||||
<br>
|
||||
2019-07-05
|
||||
</div>
|
||||
|
||||
---
|
||||
|
||||
# Intro
|
||||
- I'm not an expert on the field, neither a mathematician. Just an engineer with interest for cryptography
|
||||
- Short talk (15 min), with the objective to make a practical introduction to the Shamir's Secret Sharing algorithm
|
||||
- Is not a talk about mathematical demostrations, is a talk with the objective to get the basic notions to be able to do a practical implementation of the algorithm
|
||||
- After the talk, we will do a practical workshop to implement the concepts. We can offer support for Go, Rust, Python and Nodejs (you can choose any other language, but we will not be able to help)
|
||||
|
||||
---
|
||||
|
||||
- Cryptographic algorithm
|
||||
- Created by Adi Shamir, in 1979
|
||||
- also known by the $RSA$ cryptosystem
|
||||
- explained in few months ago in a similar talk: https://github.com/arnaucube/slides/rsa
|
||||
|
||||
---
|
||||
## What's this about?
|
||||
- imagine having a password that you want to share with 5 persons, in a way that they need to join their parts to get the original password
|
||||
- take the password, split it in 5 parts, and give one part to each one
|
||||
- when they need to recover it, they just need to get together, put all the pieces and recover the password (the `secret`)
|
||||
- this, has the problem that if a person looses its part, the secret will not be recovered anymore.. luckly we have a solution here:
|
||||
|
||||
---
|
||||
|
||||
- Shamir's Secret Sharing:
|
||||
- from a secret to be shared, we generate 5 parts, but we can specify a number of parts that are needed to recover the secret
|
||||
- so for example, we generate 5 parts, where we will need only 3 of that 5 parts to recover the secret, and the order doesn't matter
|
||||
- we have the ability to define the thresholds of $M$ parts to be created, and $N$ parts to be able the recover
|
||||
|
||||
---
|
||||
|
||||
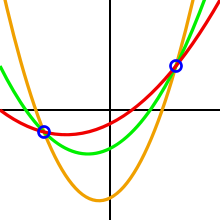
- 2 points are sufficient to define a line
|
||||
- 3 points are sufficient to define a parabola
|
||||
- 4 points are sufficient to define a cubic curve
|
||||
- $K$ points are suficient to define a polynomial of degree $k-1$
|
||||
|
||||
We can create infinity of polynomials of degree 2, that goes through 2 points, but with 3 points, we can define a polynomial of degree 2 unique.
|
||||
|
||||
|
||||
|
||||
---
|
||||
|
||||
## Naming
|
||||
|
||||
- `s`: secret
|
||||
- `m`: number of parts to be created
|
||||
- `n`: number of minimum parts necessary to recover the secret
|
||||
- `p`: random prime number, the Finite Field will be over that value
|
||||
|
||||
---
|
||||
|
||||
## Secret generation
|
||||
- we want that are necessary $n$ parts of $m$ to recover $s$
|
||||
- where $n<m$
|
||||
- need to create a polynomial of degree $n-1$
|
||||
$f(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2 + \alpha_3 x^3 + ... + + \alpha_{n-1} x^{n-1}$
|
||||
- where $\alpha_0$ is the secret $s$
|
||||
- $\alpha_i$ are random values that build the polynomial
|
||||
*where $\alpha_0$ is the secret to share, and $\alpha_i$ are the random values inside the $Finite Field$
|
||||
|
||||
---
|
||||
|
||||
$f(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2 + \alpha_3 x^3 + ... + + \alpha_{n-1} x^{n-1}$
|
||||
|
||||
- the packets that we will generate are $P = (x, f(x))$
|
||||
- where $x$ is each one of the values between $1$ and $m$
|
||||
- $P_1=(1, f(1))$
|
||||
- $P_2=(2, f(2))$
|
||||
- $P_3=(3, f(3))$
|
||||
- ...
|
||||
- $P_m=(m, f(m))$
|
||||
|
||||
---
|
||||
## Secret recovery
|
||||
- in order to recover the secret $s$, we will need a minimum of $n$ points of the polynomial
|
||||
- the order doesn't matter
|
||||
- with that $n$ parts, we do Lagrange Interpolation/Polynomial Interpolation
|
||||
|
||||
---
|
||||
|
||||
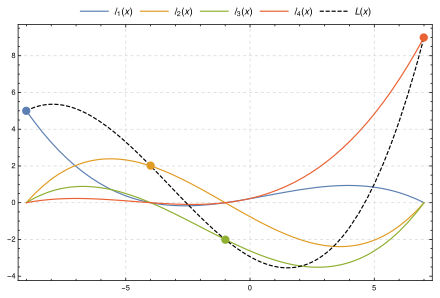
## Polynomial Interpolation / Lagrange Interpolation
|
||||
- for a group of points, we can find the smallest degree polynomial that goees through all that points
|
||||
- this polynomial is unique for each group of points
|
||||
|
||||
|
||||
|
||||
---
|
||||
|
||||

|
||||
|
||||
---
|
||||
|
||||
$L(x) = \sum_{j=0}^{n} y_j l_j(x)$
|
||||
|
||||
<br><br>
|
||||
|
||||

|
||||
|
||||
---
|
||||
|
||||
## Wikipedia example
|
||||
*example over real numbers, in the practical world, we use the algorithm in the Finite Field over $p$
|
||||
<span style="font-size:70%;float:right;">(more details: https://en.wikipedia.org/wiki/Shamir's_Secret_Sharing#Problem)</span><br>
|
||||
- $s=1234$
|
||||
- $m=6$
|
||||
- $n=3$
|
||||
- $f(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2$
|
||||
- $\alpha_0 = s = 1234$
|
||||
- $\alpha_1 = 166$ *(random)*
|
||||
- $\alpha_2 = 94$ *(random)*
|
||||
- $f(x) = 1234 + 166 x + 94 x^2$
|
||||
|
||||
---
|
||||
|
||||
- $f(x) = 1234 + 166 x + 94 x^2$
|
||||
- we calculate the points $P = (x, f(x))$
|
||||
- where $x$ is each one of the values between $1$ and $m$
|
||||
- $P_1=(1, f(1)) = (1, 1494)$
|
||||
- $P_2=(2, f(2)) = (2, 1942)$
|
||||
- $P_3=(3, f(3)) = (3, 2578)$
|
||||
- $P_4=(4, f(4)) = (4, 3402)$
|
||||
- $P_5=(5, f(5)) = (5, 4414)$
|
||||
- $P_6=(6, f(6)) = (6, 5614)$
|
||||
---
|
||||
|
||||
- to recover the secret, let's imagine that we take the packets 2, 4, 5
|
||||
- $(x_0, y_0) = (2, 1942)$
|
||||
- $(x_0, y_0) = (4, 3402)$
|
||||
- $(x_0, y_0) = (5, 4414)$
|
||||
|
||||
---
|
||||
|
||||
- let's calculate the Lagrange Interpolation
|
||||
- 
|
||||
- 
|
||||
- 
|
||||
- 
|
||||
- obtaining $f(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2$, where $\alpha_0$ is the secret $s$ recovered
|
||||
- where we eavluate the polynomial at $f(0)$, obtaining $\alpha_0 = s$
|
||||
- *we are not going into details now, but if you want in the practical workshop we can analyze the 'mathematical' part of all of this
|
||||
|
||||
---
|
||||
|
||||
# And now... practical implementation
|
||||
- full night long
|
||||
- big ints are your friends
|
||||
- $L(x) = \sum_{j=0}^{n} y_j l_j(x)$
|
||||

|
||||
|
||||
# About
|
||||
|
||||
<img src="https://arnaucube.com/img/logoArnauCubeTransparent.png" style="max-width:20%; float:right;" />
|
||||
|
||||
- https://arnaucube.com
|
||||
- https://github.com/arnaucube
|
||||
- https://twitter.com/arnaucube
|
||||
<br>
|
||||
<div style="float:right;font-size:80%;">
|
||||
<a href="https://creativecommons.org/licenses/by-nc-sa/4.0/"><img src="https://licensebuttons.net/l/by-nc-sa/4.0/88x31.png" /></a>
|
||||
<br>
|
||||
2019-07-05
|
||||
</div>
|
||||
@@ -0,0 +1,8 @@
|
||||
module demo
|
||||
|
||||
go 1.12
|
||||
|
||||
require (
|
||||
github.com/arnaucube/go-snark v0.0.4 // indirect
|
||||
github.com/stretchr/testify v1.4.0 // indirect
|
||||
)
|
||||
@@ -0,0 +1,15 @@
|
||||
github.com/arnaucube/go-snark v0.0.4 h1:JJbQx/wg0u1mzJk9Of/rqCkclPgXuvPrLWHfvgnoyEE=
|
||||
github.com/arnaucube/go-snark v0.0.4/go.mod h1:m1VkAgz3F+Jdighf2n5eMLe670AR6fBhBGfVHwz2QRk=
|
||||
github.com/davecgh/go-spew v1.1.0/go.mod h1:J7Y8YcW2NihsgmVo/mv3lAwl/skON4iLHjSsI+c5H38=
|
||||
github.com/davecgh/go-spew v1.1.1 h1:vj9j/u1bqnvCEfJOwUhtlOARqs3+rkHYY13jYWTU97c=
|
||||
github.com/davecgh/go-spew v1.1.1/go.mod h1:J7Y8YcW2NihsgmVo/mv3lAwl/skON4iLHjSsI+c5H38=
|
||||
github.com/pmezard/go-difflib v1.0.0 h1:4DBwDE0NGyQoBHbLQYPwSUPoCMWR5BEzIk/f1lZbAQM=
|
||||
github.com/pmezard/go-difflib v1.0.0/go.mod h1:iKH77koFhYxTK1pcRnkKkqfTogsbg7gZNVY4sRDYZ/4=
|
||||
github.com/stretchr/objx v0.1.0/go.mod h1:HFkY916IF+rwdDfMAkV7OtwuqBVzrE8GR6GFx+wExME=
|
||||
github.com/stretchr/testify v1.2.2/go.mod h1:a8OnRcib4nhh0OaRAV+Yts87kKdq0PP7pXfy6kDkUVs=
|
||||
github.com/stretchr/testify v1.4.0 h1:2E4SXV/wtOkTonXsotYi4li6zVWxYlZuYNCXe9XRJyk=
|
||||
github.com/stretchr/testify v1.4.0/go.mod h1:j7eGeouHqKxXV5pUuKE4zz7dFj8WfuZ+81PSLYec5m4=
|
||||
github.com/urfave/cli v1.20.0/go.mod h1:70zkFmudgCuE/ngEzBv17Jvp/497gISqfk5gWijbERA=
|
||||
gopkg.in/check.v1 v0.0.0-20161208181325-20d25e280405/go.mod h1:Co6ibVJAznAaIkqp8huTwlJQCZ016jof/cbN4VW5Yz0=
|
||||
gopkg.in/yaml.v2 v2.2.2 h1:ZCJp+EgiOT7lHqUV2J862kp8Qj64Jo6az82+3Td9dZw=
|
||||
gopkg.in/yaml.v2 v2.2.2/go.mod h1:hI93XBmqTisBFMUTm0b8Fm+jr3Dg1NNxqwp+5A1VGuI=
|
||||
109
src/zksnarks-from-scratch-a-technical-explanation/demo/main.go
Normal file
@@ -0,0 +1,109 @@
|
||||
package main
|
||||
|
||||
import (
|
||||
"encoding/json"
|
||||
"fmt"
|
||||
"math/big"
|
||||
"strings"
|
||||
"time"
|
||||
|
||||
"github.com/arnaucube/go-snark"
|
||||
"github.com/arnaucube/go-snark/circuitcompiler"
|
||||
)
|
||||
|
||||
func main() {
|
||||
// circuit function
|
||||
// y = x^5 + 2*x + 6
|
||||
code := `
|
||||
func exp5(private a):
|
||||
b = a * a
|
||||
c = a * b
|
||||
d = a * c
|
||||
e = a * d
|
||||
return e
|
||||
|
||||
func main(private s0, public s1):
|
||||
s2 = exp5(s0)
|
||||
s3 = s0 * 2
|
||||
s4 = s3 + s2
|
||||
s5 = s4 + 6
|
||||
equals(s1, s5)
|
||||
out = 1 * 1
|
||||
`
|
||||
fmt.Print("\ncode of the circuit:")
|
||||
fmt.Println(code)
|
||||
|
||||
// parse the code
|
||||
parser := circuitcompiler.NewParser(strings.NewReader(code))
|
||||
circuit, err := parser.Parse()
|
||||
if err != nil {
|
||||
panic(err)
|
||||
}
|
||||
fmt.Println("\ncircuit data:", circuit)
|
||||
circuitJson, _ := json.Marshal(circuit)
|
||||
fmt.Println("circuit:", string(circuitJson))
|
||||
|
||||
b8 := big.NewInt(int64(8))
|
||||
privateInputs := []*big.Int{b8}
|
||||
b32790 := big.NewInt(int64(32790))
|
||||
publicSignals := []*big.Int{b32790}
|
||||
|
||||
// wittness
|
||||
w, err := circuit.CalculateWitness(privateInputs, publicSignals)
|
||||
if err != nil {
|
||||
panic(err)
|
||||
}
|
||||
|
||||
// code to R1CS
|
||||
fmt.Println("\ngenerating R1CS from code")
|
||||
a, b, c := circuit.GenerateR1CS()
|
||||
fmt.Println("\nR1CS:")
|
||||
fmt.Println("a:", a)
|
||||
fmt.Println("b:", b)
|
||||
fmt.Println("c:", c)
|
||||
|
||||
// R1CS to QAP
|
||||
// TODO zxQAP is not used and is an old impl, TODO remove
|
||||
alphas, betas, gammas, _ := snark.Utils.PF.R1CSToQAP(a, b, c)
|
||||
fmt.Println("qap")
|
||||
fmt.Println(alphas)
|
||||
fmt.Println(betas)
|
||||
fmt.Println(gammas)
|
||||
|
||||
_, _, _, px := snark.Utils.PF.CombinePolynomials(w, alphas, betas, gammas)
|
||||
|
||||
// calculate trusted setup
|
||||
setup, err := snark.GenerateTrustedSetup(len(w), *circuit, alphas, betas, gammas)
|
||||
if err != nil {
|
||||
panic(err)
|
||||
}
|
||||
fmt.Println("\nt:", setup.Toxic.T)
|
||||
|
||||
// zx and setup.Pk.Z should be the same (currently not, the correct one is the calculation used inside GenerateTrustedSetup function), the calculation is repeated. TODO avoid repeating calculation
|
||||
|
||||
proof, err := snark.GenerateProofs(*circuit, setup.Pk, w, px)
|
||||
if err != nil {
|
||||
panic(err)
|
||||
}
|
||||
|
||||
fmt.Println("\n proofs:")
|
||||
fmt.Println(proof)
|
||||
|
||||
// fmt.Println("public signals:", proof.PublicSignals)
|
||||
fmt.Println("\nsignals:", circuit.Signals)
|
||||
fmt.Println("witness:", w)
|
||||
b32790Verif := big.NewInt(int64(32790))
|
||||
publicSignalsVerif := []*big.Int{b32790Verif}
|
||||
before := time.Now()
|
||||
if !snark.VerifyProof(setup.Vk, proof, publicSignalsVerif, true) {
|
||||
fmt.Println("Verification not passed")
|
||||
}
|
||||
fmt.Println("verify proof time elapsed:", time.Since(before))
|
||||
|
||||
// check that with another public input the verification returns false
|
||||
bOtherWrongPublic := big.NewInt(int64(34))
|
||||
wrongPublicSignalsVerif := []*big.Int{bOtherWrongPublic}
|
||||
if snark.VerifyProof(setup.Vk, proof, wrongPublicSignalsVerif, true) {
|
||||
fmt.Println("Verification should not have passed")
|
||||
}
|
||||
}
|
||||
|
After Width: | Height: | Size: 190 KiB |
|
After Width: | Height: | Size: 72 KiB |
|
After Width: | Height: | Size: 61 KiB |
|
After Width: | Height: | Size: 73 KiB |
|
After Width: | Height: | Size: 23 KiB |
|
After Width: | Height: | Size: 47 KiB |
|
After Width: | Height: | Size: 9.0 KiB |
BIN
src/zksnarks-from-scratch-a-technical-explanation/imgs/iden3.png
Normal file
|
After Width: | Height: | Size: 4.6 KiB |
|
After Width: | Height: | Size: 269 KiB |
|
After Width: | Height: | Size: 16 KiB |
@@ -0,0 +1 @@
|
||||
<mxfile modified="2019-08-13T18:47:10.347Z" host="www.draw.io" agent="Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/75.0.3770.142 Safari/537.36" etag="g-j6-4IYbbkWM6JlDttD" version="11.1.4" type="device"><diagram id="gLyV9NRtU4jVRmGOj88S" name="Page-1">5Vldb5swFP01edyEMRDy2NCvSZu0Ldu6Pk0OXMCtwcgxTbJfPwMmQKFdqpGiqalUcY99zeX4HMglM+wluytBsvgTD4DNTCPYzfD5zDTxHKn/BbCvgLnhVkAkaFBBqAFW9Ddo0NBoTgPYdCZKzpmkWRf0eZqCLzsYEYJvu9NCzrpnzUgEPWDlE9ZHb2ggY40iw2gGroFGsT61a+uBhNSTNbCJScC3LQhfzLAnOJfVUbLzgBXc1bxUeZdPjB4KE5DKYxJ+ba6tm/P766UHd/g7OeN3Hx7emdUqD4Tl+oJ1sXJfMyB4ngZQLGLM8HIbUwmrjPjF6FZtucJimTAVIXWolwMhYfdknehw9Uo1wBOQYq+m6ISF5ksLBjk63rbor+fELeaRpUGitzw6LN2wog40MS8gyelxAoESiQ65kDGPeErYRYMuu6w1cz5ynmmu7kDKvVY8ySUfYrI40fM8qrp4Lnx4pn6sfUNEBPKZedbwvghgRNKHbh2jk4x7SrxUp5WQKhJLe2+kIDSVm38TaEgZ8zjjoszFoeuD7ytcrc7voTWydm3LNsaRNEKPNL0Y0LQ9oGl8KkkvppA07Kj8WaS/t3V02xo53+mVy2BfB6m63FZSEd62x5q0MqrzRrSPdaR93CntY/Xs8xV5q3G9EoIz7JVgvlgbY3nFsjteMW275xX3Na2C8CRemV737pG6R+aUwnd7wv9y9nlk3YfmE7p31o7tnEb32Jxa96jH4tvQff2w/qvw8ZS6r6tsCd9Tzde4yreLvyHlO+WnyOCpbOHV5zSOOHyLmswR9lt1hHnso2DSFqIus2WJbyLfyLKDWIHMs1HdEdjgBtaQO1xzjZ2xngu42ztgt/9cODjjdWwwn8QG/2fzgI7tHpAzqXX6/cNnwXmooCvVggtVAk/HdQ8BNxz8VuX4LqzD07jHsiZ3j9Nj+gcIGlJ/fI4BqXvUfIjjhTPH5ER3KNuYnON+U+BR4edUlq+SkowyED2mFQOyS2eXtpSn8IhjDRFGo1SFvmJMLYyXBZ9qQ9mZHkhoEJS3waH96+7wGBtyxCvUoTeo5sv3Q4XNG+xyrPUzAL74Aw==</diagram></mxfile>
|
||||
|
After Width: | Height: | Size: 13 KiB |
@@ -0,0 +1 @@
|
||||
<mxfile modified="2019-08-13T18:56:28.989Z" host="www.draw.io" agent="Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/75.0.3770.142 Safari/537.36" etag="eB5zEFUdvqCOVYVfGWWE" version="11.1.4" type="device"><diagram id="ifYI8tIDXpRssO3bx3ur" name="Page-1">5Vhdb5swFP01eexEMB/u45p267TuQ4vWdo8OXMCbw40ck4/9+hliCBQSpRJJGg0e8D32NebccyyLARlNVx8lmyVfMAQxsK1wNSC3A9se2o6jHzmy3iC+RTdALHloBm2BMf8LBrQMmvEQ5o2BClEoPmuCAaYpBKqBMSlx2RwWoWi+dcZiaAHjgIk2+sRDlRh0aFnbjnvgcWJeTV3TMWXlYAPMExbisgaRuwEZSUS1aU1XIxA5eSUvm7wPO3qrhUlI1SEJ2dXDeArBjX/z4+f9+69OFH17vKoWp9blF0OoCTBhiql+3EjM0hDyeSwdoVQJxpgy8YA40+BQg79BqbUpH8sUaihRU2F6YcXVc639K5/qnWui25WZuQjWZZAquX6uB7WsPNymFVGZt/mg/Ct2EmWgOWYygD3slIJjMga1Zxytyql9ADgFvR6dJ0EwxRfNdTAjyLgat62ZbpiyvaKEZt4FE5l503eJC5CtwjaruEy4gvGMFQQstXmbFYu4ECMUKItcErn5rfG5kvgHaj1eceUZmKoavrmqeugFKVjtr0ibQZNQ7QZmE7EtV8ugQJY1U5aeTGp+HDrWsXj3Ls469gm9Yx/onR2VP4137A7v8AVToMFP6SxT835dRAMIgi4XTajruFY/biEvzWIdZhVyNKf4b9YpPQqeXILgSVvw2UTw4Dh6h2Hogt+l92vPJ8w7jt6ds+ud/g96dy9B725L709cpTDvV+da5TR0unRO7QnxjqRzenadX79Zne86AfknPAH5l2AQv+MEhAuexhr8DOt+jz9RZHcff0Jv4rnHsQmxz20T2kUxRv3uQAxo1EmtF1CYRD1RS19sQS49kFv31dzqcPtvpOir/WEid/8A</diagram></mxfile>
|
||||
|
After Width: | Height: | Size: 9.5 KiB |
@@ -0,0 +1 @@
|
||||
<mxfile modified="2019-08-13T18:59:55.608Z" host="www.draw.io" agent="Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/75.0.3770.142 Safari/537.36" etag="6NXsGmdxVBTOZbGWR0NA" version="11.1.4" type="device"><diagram id="ifYI8tIDXpRssO3bx3ur" name="Page-1">3Vdbk5owFP41Pm4HiFz66OpeOt12O+vspU+dCAfIGhImBJX++gYMCuI6bqvrWHwg5zvnJPE7+ZLQQ8NkcSNwGn/jAdCeZQSLHhr1LMu0+n31KpFiibiGtwQiQQIdtAbG5Ddo0NBoTgLIWoGScypJ2gZ9zhj4soVhIfi8HRZy2h41xRF0gLGPaRd9JoGMNWoaxtpxCySK9dCerR0JroM1kMU44PMGhK56aCg4l8tWshgCLcmreVnmXb/hXU1MAJP7JOQXd+ME/Ev38uHxdvC9H4b3Txerycmi/scQKAK0yThTr0vBcxZA2Y+hLC5kzCPOML3jPFWgqcBXkLLQ5cO55AqKZUK1FxZEvjTaP8uuPtnaGi10z5VR1AaTonhpGo2s0lynVVad1+VFU5XxXPiwg4x6fWERgdwRp1dwSVRjAM36DfAE1HxUgACKJZm1VxLWCzJaxa1rphq6bO8ooe53hmmuR3oCQUIColPadh3nMZEwTnHFyVzJt12zkFA65JSLKheFdvlTeCYFn0LD41RPmcGZbODLZ1dFZiAkLHZyqL2r/UBvI5Zhq4VQIfOGLGtVxg1Fmn3j35k3H/GgIKPrXwPnNUumLJzkDzXzbxJ8YqFY+yllYxn/nXTQntI5qVJQRyk/8gklvsK+sDSX2UEFA2Zgg7tNMJ8dF2HnMMJAG7qwjH11gY4lC+s/PVIOIhT7HIRid4Wi7inhQeURYPBCf+t54nswCY8jD+f08kBnJw/3A/XhnoM+3O1XroKwSMFfoTjszSsMLX+rUgJn4tjHOUiQ8aFK2XXPbtB8Pz3HPcjb2IRsb09i7XcTq8z1F2Xla3yXo6s/</diagram></mxfile>
|
||||
@@ -0,0 +1,877 @@
|
||||
# zkSNARKs from scratch, a technical explanation
|
||||
|
||||
<br><br><br>
|
||||
<div style="float:right; text-align:right;">
|
||||
<img style="width:80px" src="imgs/arnaucube.png" /> <br>
|
||||
|
||||
[arnaucube.com](https://arnaucube.com)
|
||||
[github.com/arnaucube](https://github.com/arnaucube)
|
||||
[twitter.com/arnaucube](https://twitter.com/arnaucube)
|
||||
<br>
|
||||
<a href="https://creativecommons.org/licenses/by-nc-sa/4.0/"><img src="https://licensebuttons.net/l/by-nc-sa/4.0/88x31.png" /></a>
|
||||
2019-08-20
|
||||
</div>
|
||||
|
||||
<img style="width:200px;" src="imgs/iden3.png" /> <br>
|
||||
[iden3.io](https://iden3.io)
|
||||
[github.com/iden3](https://github.com/iden3)
|
||||
[twitter.com/identhree](https://twitter.com/identhree)
|
||||
|
||||
|
||||
---
|
||||
|
||||
## Warning
|
||||
|
||||
<div style="font-size:90%;">
|
||||
|
||||
- I'm not a mathematician, this talk is not for mathematicians
|
||||
|
||||
- In free time, have been studying zkSNARKS & implementing it in Go
|
||||
|
||||
- Talk about a technical explaination from an engineer point of view
|
||||
- The idea is to try to transmit the learnings from long night study hours during last winter
|
||||
- Also at the end will briefly overview how we use zkSNARKs in iden3
|
||||
- This slides will be combined with
|
||||
- parts of the code from https://github.com/arnaucube/go-snark
|
||||
- whiteboard draws and writtings
|
||||
- Don't use your own crypto. But it's fun to implement it (only for learning purposes)
|
||||
|
||||
</div>
|
||||
|
||||
---
|
||||
|
||||
## Contents
|
||||
|
||||
<div style="font-size: 90%;">
|
||||
|
||||
- Introduction
|
||||
- zkSNARK overview
|
||||
- zkSNARK flow
|
||||
- Generating and verifying proofs
|
||||
- Foundations
|
||||
- Basics of modular arithmetic
|
||||
- Groups
|
||||
- Finite fields
|
||||
- Elliptic curve operations
|
||||
- Pairings
|
||||
- Bilinear Pairings
|
||||
- BLS signatures
|
||||
|
||||
</div>
|
||||
|
||||
---
|
||||
|
||||
<div style="font-size: 90%;">
|
||||
|
||||
- zkSNARK (Pinocchio)
|
||||
- Circuit compiler
|
||||
- R1CS
|
||||
- QAP
|
||||
- Lagrange Interpolation
|
||||
- Trusted Setup
|
||||
- Proofs generation
|
||||
- Proofs verification
|
||||
- Groth16
|
||||
- How we use zkSNARKs in iden3
|
||||
- libraries
|
||||
- Circuit languages
|
||||
- utilities (Elliptic curve & Hash functions) inside the zkSNARK libraries
|
||||
- BabyJubJub
|
||||
- Mimc
|
||||
- Poseidon
|
||||
- References
|
||||
|
||||
</div>
|
||||
|
||||
---
|
||||
|
||||
## Introduction
|
||||
- zero knowledge concept
|
||||
- examples
|
||||
- some concept explanations
|
||||
- https://en.wikipedia.org/wiki/Zero-knowledge_proof
|
||||
- https://hackernoon.com/wtf-is-zero-knowledge-proof-be5b49735f27
|
||||
|
||||
---
|
||||
|
||||
|
||||
## zkSNARK overview
|
||||
|
||||
|
||||
- protocol to prove the correctness of a computation
|
||||
- useful for
|
||||
- scalability
|
||||
- privacy
|
||||
- interoperability
|
||||
- examples:
|
||||
- Alice can prove to Brenna that knows $x$ such as $f(x) = y$
|
||||
- Brenna can prove to Alice that knows a certain input which $Hash$ results in a certain known value
|
||||
- Carol can proof that is a member of an organization without revealing their identity
|
||||
- etc
|
||||
|
||||
---
|
||||
|
||||
### zkSNARK flow
|
||||
|
||||
<div style="text-align:center;">
|
||||
<img src="imgs/zksnark-concept-flow.png"/>
|
||||
</div>
|
||||
|
||||
---
|
||||
|
||||
|
||||
### Generating and verifying proofs
|
||||
Generating a proof:
|
||||
|
||||
<img src="imgs/zksnark-prover.png"/>
|
||||
|
||||
<img src="imgs/cat04.jpeg" style="float:right; width:300px;" />
|
||||
|
||||
<br><br>
|
||||
|
||||
Verifying a proof:
|
||||
|
||||
<img src="imgs/zksnark-verifier.png"/>
|
||||
|
||||
|
||||
|
||||
|
||||
---
|
||||
|
||||
|
||||
## Foundations
|
||||
- Modular aritmetic
|
||||
- Groups
|
||||
- Finite fields
|
||||
- Elliptic Curve Cryptography
|
||||
|
||||
---
|
||||
|
||||
## Basics of modular arithmetic
|
||||
- Modulus, `mod`, `%`
|
||||
- Remainder after division of two numbers
|
||||
|
||||

|
||||
|
||||
```python
|
||||
5 mod 12 = 5
|
||||
14 mod 12 = 2
|
||||
83 mod 10 = 3
|
||||
```
|
||||
|
||||
```python
|
||||
5 + 3 mod 6 = 8 mod 6 = 2
|
||||
```
|
||||
|
||||
|
||||
---
|
||||
|
||||
## Groups
|
||||
- a **set** with an **operation**
|
||||
- **operation** must be *associative*
|
||||
- neutral element ($identity$): adding the neutral element to any element gives the element
|
||||
- inverse: $e$ + $e_{inverse}$ = $identity$
|
||||
- cyclic groups
|
||||
- finite group with a generator element
|
||||
- any element must be writable by a multiple of the generator element
|
||||
- abelian group
|
||||
- group with *commutative* operation
|
||||
|
||||
---
|
||||
|
||||
## Finite fields
|
||||
- algebraic structure like Groups, but with **two operations**
|
||||
- extended fields concept (https://en.wikipedia.org/wiki/Field_extension)
|
||||
|
||||
---
|
||||
|
||||
## Elliptic curve
|
||||
- point addition
|
||||
|
||||
$(x_1, y_1) + (x_2, y_2) =
|
||||
(\dfrac{
|
||||
x_1 y_2 + x_2 y_1
|
||||
}{
|
||||
1 + d x_1 x_2 y_1 y_2
|
||||
},
|
||||
\dfrac{
|
||||
y_1 y_2 - x_1 x_2
|
||||
}{
|
||||
1-dx_1 x_2 y_1 y_2
|
||||
})$
|
||||
- G1
|
||||
- G2
|
||||
|
||||
*(whiteboard explanation)*
|
||||
|
||||
---
|
||||
|
||||
## Pairings
|
||||
- 3 typical types used for SNARKS:
|
||||
- BN (Barreto Naehrig) - used in Ethereum
|
||||
- BLS (Barreto Lynn Scott) - used in ZCash & Ethereum 2.0
|
||||
- MNT (Miyaji- Nakabayashi - Takano) - used in CodaProtocol
|
||||
- $y^2 = x^3 + b$ with embedding degree 12
|
||||
- function that maps (pairs) two points from sets `S1` and `S2` into another set `S3`
|
||||
- is a [bilinear](https://en.wikipedia.org/wiki/Bilinear_map) function
|
||||
- $e(G_1, G_2) -> G_T$
|
||||
- the groups must be
|
||||
- cyclic
|
||||
- same prime order ($r$)
|
||||
|
||||
---
|
||||
|
||||
- $F_q$, where $q=$`21888242871839275222246405745257275088696311157297823662689037894645226208583`
|
||||
- $F_r$, where $r=$`21888242871839275222246405745257275088548364400416034343698204186575808495617`
|
||||
|
||||
---
|
||||
|
||||
## Bilinear Pairings
|
||||
$e(P_1 + P_2, Q_1) == e(P_1, Q_1) \cdot e(P_2, Q_1)$
|
||||
|
||||
$e(P_1, Q_1 + Q_2) == e(P_1, Q_1) \cdot e(P_1, Q_2)$
|
||||
|
||||
$e(aP, bQ) == e(P, Q)^{ab} == e(bP, aQ)$
|
||||
|
||||
<img src="imgs/cat01.jpeg" style="float:right; width:300px;" />
|
||||
|
||||
$e(g_1, g_2)^6 == e(g_1, 6 \cdot g_2)$
|
||||
|
||||
$e(g_1, g_2)^6 == e(6 \cdot g_1, g_2)$
|
||||
|
||||
$e(g_1, g_2)^6 == e(3 \cdot g_1, 2 g_2)$
|
||||
|
||||
$e(g_1, g_2)^6 == e(2 \cdot g_1, 3 g_2)$
|
||||
|
||||
|
||||
---
|
||||
|
||||
### BLS signatures
|
||||
*(small overview, is offtopic here, but is interesting)*
|
||||
- key generation
|
||||
- random private key $x$ in $[0, r-1]$
|
||||
- public key $g^x$
|
||||
- signature
|
||||
- $h=Hash(m)$ (over G2)
|
||||
- signature $\sigma=h^x$
|
||||
- verification
|
||||
- check that: $e(g, \sigma) == e(g^x, Hash(m))$
|
||||
$e(g, h^x) == e(g^x, h)$
|
||||
|
||||
|
||||
---
|
||||
|
||||
- aggregate signatures
|
||||
- $s = s0 + s1 + s2 ...$
|
||||
- verify aggregated signatures
|
||||
|
||||
<div style="font-size:75%">
|
||||
|
||||
$e(G,S) == e(P, H(m))$
|
||||
|
||||
$e(G, s0+s1+s2...) == e(p0, H(m)) \cdot e(p1, H(m)) \cdot e(p2, H(m)) ...$
|
||||
|
||||
</div>
|
||||
|
||||
|
||||
More info: https://crypto.stanford.edu/~dabo/pubs/papers/BLSmultisig.html
|
||||
|
||||
---
|
||||
|
||||
## Circuit compiler
|
||||
- not a software compiler -> a constraint prover
|
||||
- what this means
|
||||
- constraint concept
|
||||
- `value0` == `value1` `<operation>` `value2`
|
||||
- want to proof that a certain computation has been done correctly
|
||||
- graphic of circuit with gates (whiteboard)
|
||||
|
||||
- about high level programing languages for zkSNARKS, by *Harry Roberts*: https://www.youtube.com/watch?v=nKrBJo3E3FY
|
||||
|
||||
---
|
||||
|
||||
Circuit code example:
|
||||
$f(x) = x^5 + 2\cdot x + 6$
|
||||
|
||||
```
|
||||
func exp5(private a):
|
||||
b = a * a
|
||||
c = a * b
|
||||
d = a * c
|
||||
e = a * d
|
||||
return e
|
||||
|
||||
func main(private s0, public s1):
|
||||
s2 = exp5(s0)
|
||||
s3 = s0 * 2
|
||||
s4 = s3 + s2
|
||||
s5 = s4 + 6
|
||||
equals(s1, s5)
|
||||
out = 1 * 1
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
## Inputs and Witness
|
||||
For a certain circuit, with the inputs that we calculate the Witness for the circuit signals
|
||||
- private inputs: `[8]`
|
||||
- in this case the private input is the 'secret' $x$ value that computed into the equation gives the expected $f(x)$
|
||||
- public inputs: `[32790]`
|
||||
- in this case the public input is the result of the equation
|
||||
- signals: `[one s1 s0 b0 c0 d0 s2 s3 s4 s5 out]`
|
||||
- witness: `[1 32790 8 64 512 4096 32768 16 32784 32790 1]`
|
||||
|
||||
---
|
||||
|
||||
## R1CS
|
||||
- Rank 1 Constraint System
|
||||
- way to write down the constraints by 3 linear combinations
|
||||
- 1 constraint per operation
|
||||
- $(A, B, C) = A.s \cdot B.s - C.s = 0$
|
||||
- from flat code constraints we can generate the R1CS
|
||||
|
||||
---
|
||||
|
||||
## R1CS
|
||||
|
||||
<div style="font-size:65%">
|
||||
|
||||
$(a_{11}s_1 + a_{12}s_2 + ... + a_{1n}s_n) \cdot (b_{11}s_1 + b_{12}s_2 + ... + b_{1n}s_n) - (c_{11}s_1 + c_{12}s_2 + ... + c_{1n}s_n) = 0$
|
||||
|
||||
$(a_{21}s_1 + a_{22}s_2 + ... + a_{2n}s_n) \cdot (b_{21}s_1 + b_{22}s_2 + ... + b_{2n}s_n) - (c_{21}s_1 + c_{22}s_2 + ... + c_{2n}s_n) = 0$
|
||||
$(a_{31}s_1 + a_{32}s_2 + ... + a_{3n}s_n) \cdot (b_{31}s_1 + b_{32}s_2 + ... + b_{3n}s_n) - (c_{31}s_1 + c_{32}s_2 + ... + c_{3n}s_n) = 0$
|
||||
[...]
|
||||
$(a_{m1}s_1 + a_{m2}s_2 + ... + a_{mn}s_n) \cdot (b_{m1}s_1 + b_{m2}s_2 + ... + b_{mn}s_n) - (c_{m1}s_1 + c_{m2}s_2 + ... + c_{mn}s_n) = 0$
|
||||
|
||||
*where $s$ are the signals of the circuit, and we need to find $a, b, c$ that satisfies the equations
|
||||
</div>
|
||||
|
||||
---
|
||||
|
||||
R1CS constraint example:
|
||||
- signals: `[one s1 s0 b0 c0 d0 s2 s3 s4 s5 out]`
|
||||
- witness: `[1 32790 8 64 512 4096 32768 16 32784 32790 1]`
|
||||
- First constraint flat code: `b0 == s0 * s0`
|
||||
- R1CS first constraint:
|
||||
$A_1 = [00100000000]$
|
||||
$B_1 = [00100000000]$
|
||||
$C_1 = [00010000000]$
|
||||
|
||||
---
|
||||
|
||||
R1CS example:
|
||||
|
||||
| $A$| $B$ | $C$: |
|
||||
|-|-|-|
|
||||
| $[0 0 1 0 0 0 0 0 0 0 0]$<br>$[0 0 1 0 0 0 0 0 0 0 0]$<br>$[0 0 1 0 0 0 0 0 0 0 0]$<br>$[0 0 1 0 0 0 0 0 0 0 0]$<br>$[0 0 1 0 0 0 0 0 0 0 0]$<br>$[0 0 0 0 0 0 1 1 0 0 0]$<br>$[6 0 0 0 0 0 0 0 1 0 0]$<br>$[0 0 0 0 0 0 0 0 0 1 0]$<br>$[0 1 0 0 0 0 0 0 0 0 0]$<br>$[1 0 0 0 0 0 0 0 0 0 0]$ | $[0 0 1 0 0 0 0 0 0 0 0]$<br>$[0 0 0 1 0 0 0 0 0 0 0]$<br>$[0 0 0 0 1 0 0 0 0 0 0]$<br>$[0 0 0 0 0 1 0 0 0 0 0]$<br>$[2 0 0 0 0 0 0 0 0 0 0]$<br>$[1 0 0 0 0 0 0 0 0 0 0]$<br>$[1 0 0 0 0 0 0 0 0 0 0]$<br>$[1 0 0 0 0 0 0 0 0 0 0]$<br>$[1 0 0 0 0 0 0 0 0 0 0]$<br>$[1 0 0 0 0 0 0 0 0 0 0]$ | $[0 0 0 1 0 0 0 0 0 0 0]$ <br>$[0 0 0 0 1 0 0 0 0 0 0]$<br>$[0 0 0 0 0 1 0 0 0 0 0]$<br>$[0 0 0 0 0 0 1 0 0 0 0]$<br>$[0 0 0 0 0 0 0 1 0 0 0]$<br>$[0 0 0 0 0 0 0 0 1 0 0]$<br>$[0 0 0 0 0 0 0 0 0 1 0]$<br>$[0 1 0 0 0 0 0 0 0 0 0]$<br>$[0 0 0 0 0 0 0 0 0 1 0]$<br>$[0 0 0 0 0 0 0 0 0 0 1]$ |
|
||||
|
||||
|
||||
---
|
||||
|
||||
## QAP
|
||||
- Quadratic Arithmetic Programs
|
||||
- 3 polynomials, linear combinations of R1CS
|
||||
- very good article about QAP by Vitalik Buterin https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
|
||||
|
||||
---
|
||||
|
||||

|
||||
|
||||
---
|
||||
|
||||
### Lagrange Interpolation
|
||||
(Polynomial Interpolation)
|
||||
- for a group of points, we can find the smallest degree polynomial that goees through all that points
|
||||
- this polynomial is unique for each group of points
|
||||
|
||||

|
||||
|
||||
---
|
||||
|
||||
$L(x) = \sum_{j=0}^{n} y_j l_j(x)$
|
||||
|
||||
<br><br>
|
||||
|
||||

|
||||
|
||||
|
||||
---
|
||||
|
||||
#### Shamir's Secret Sharing
|
||||
*(small overview, is offtopic here, but is interesting)*
|
||||
|
||||
- from a secret to be shared, we generate 5 parts, but we can specify a number of parts that are needed to recover the secret
|
||||
- so for example, we generate 5 parts, where we will need only 3 of that 5 parts to recover the secret, and the order doesn't matter
|
||||
- we have the ability to define the thresholds of $M$ parts to be created, and $N$ parts to be able the recover
|
||||
|
||||
---
|
||||
|
||||
##### Shamir's Secret Sharing - Secret generation
|
||||
- we want that are necessary $n$ parts of $m$ to recover $s$
|
||||
- where $n<m$
|
||||
- need to create a polynomial of degree $n-1$
|
||||
$f(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2 + \alpha_3 x^3 + ... + + \alpha_{n-1} x^{n-1}$
|
||||
- where $\alpha_0$ is the secret $s$
|
||||
- $\alpha_i$ are random values that build the polynomial
|
||||
*where $\alpha_0$ is the secret to share, and $\alpha_i$ are the random values inside the $Finite Field$
|
||||
|
||||
---
|
||||
|
||||
$f(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2 + \alpha_3 x^3 + ... + + \alpha_{n-1} x^{n-1}$
|
||||
|
||||
- the packets that we will generate are $P = (x, f(x))$
|
||||
- where $x$ is each one of the values between $1$ and $m$
|
||||
- $P_1=(1, f(1))$
|
||||
- $P_2=(2, f(2))$
|
||||
- $P_3=(3, f(3))$
|
||||
- ...
|
||||
- $P_m=(m, f(m))$
|
||||
|
||||
---
|
||||
|
||||
##### Shamir's Secret Sharing - Secret recovery
|
||||
- in order to recover the secret $s$, we will need a minimum of $n$ points of the polynomial
|
||||
- the order doesn't matter
|
||||
- with that $n$ parts, we do Lagrange Interpolation/Polynomial Interpolation, recovering the original polynomial
|
||||
|
||||
---
|
||||
|
||||
## QAP
|
||||
|
||||
<div style="font-size:50%">
|
||||
|
||||
$(\alpha_1(x)s_1 + \alpha_2(x)s_2 + ... + \alpha_n(x)s_n) \cdot (\beta_1(x)s_1 + \beta_2(x)s_2 + ... + \beta_n(x)s_n) - (\gamma_1(x)s_1 + \gamma_2(x)s_2 + ... + \gamma_n(x)s_n) = P(x)$
|
||||
|
||||
|----------------------- $A(x)$ -----------------------|------------------------ $B(x)$ -----------------------|------------------------ $C(x)$ ------------------------|
|
||||
|
||||
</div>
|
||||
|
||||
<div style="font-size:70%">
|
||||
|
||||
- $P(x) = A(x)B(x)-C(x)$
|
||||
- $P(x) = Z(x) h(x)$
|
||||
- $Z(x)$: divisor polynomial
|
||||
- $Z(x) = (x - x_1)(x-x_2)...(x-x_m) => ...=> (x_1, 0), (x_2, 0), ..., (x_m, 0)$
|
||||
- optimizations with FFT
|
||||
- $h(x) = P(x) / Z(x)$
|
||||
|
||||
</div>
|
||||
|
||||
---
|
||||
|
||||
*The following explanation is for the [Pinocchio protocol](https://eprint.iacr.org/2013/279.pdf), all the examples will be for this protocol. The [Groth16](https://eprint.iacr.org/2016/260.pdf) is explained also in the end of this slides.*
|
||||
|
||||
---
|
||||
|
||||
## Trusted Setup
|
||||
- concept
|
||||
- $\tau$ (Tau)
|
||||
- "Toxic waste"
|
||||
- Proving Key
|
||||
- Verification Key
|
||||
|
||||
---
|
||||
|
||||
$g_1 t^0, g_1 t^1, g_1 t^2, g_1 t^3, g_1 t^4, ...$
|
||||
$g_2 t^0, g_2 t^1, g_2 t^2, g_2 t^3, g_2 t^4, ...$
|
||||
|
||||
---
|
||||
|
||||
Proving Key:
|
||||
$pk = (C, pk_A, pk_A', pk_B, pk_B', pk_C, pk_C', pk_H)$ where:
|
||||
- $pk_A = \{ A_i(\tau) \rho_A P_1 \}^{m+3}_{i=0}$
|
||||
- $pk_A' = \{ A_i(\tau) \alpha_A \rho_A P_1 \}^{m+3}_{i=n+1}$
|
||||
- $pk_B = \{ B_i(\tau) \rho_B P_2 \}^{m+3}_{i=0}$
|
||||
- $pk_B' = \{ B_i(\tau) \alpha_B \rho_B P_1 \}^{m+3}_{i=0}$
|
||||
- $pk_C = \{ C_i(\tau) \rho_C P_1 \}^{m+3}_{i=0} = \{C_i(\tau) \rho_A \rho_B P_1\}^{m+3}_{i=0}$
|
||||
- $pk_C' = \{ C_i(\tau) \alpha_C \rho_C P_1 \}^{m+3}_{i=0} = \{ C_i(\tau) \alpha_C \rho_A \rho_B P_1 \}^{m+3}_{i=0}$
|
||||
- $pk_K = \{ \beta (A_i(\tau) \rho_A + B_i(\tau) \rho_B C_i(\tau) \rho_A \rho_B) P_1 \} ^{m+3}_{i=0}$
|
||||
- $pk_H = \{ \tau^i P_1 \}^d_{i=0}$
|
||||
|
||||
where:
|
||||
- $d$: degree of polynomial $Z(x)$
|
||||
- $m$: number of circuit signals
|
||||
|
||||
---
|
||||
|
||||
Verification Key:
|
||||
$vk = (vk_A, vk_B, vk_C, vk_\gamma, vk^1_{\beta\gamma}, vk^2_{\beta\gamma}, vk_Z, vk_{IC})$
|
||||
- $vk_A = \alpha_A P_2$, $vk_B = \alpha_B P_1$, $vk_C = \alpha_C P_2$
|
||||
- $vk_{\beta\gamma} = \gamma P_2$, $vk^1_{\beta\gamma} = \beta\gamma P_1$, $vk^2_{\beta\gamma} = \beta\gamma P_2$
|
||||
- $vk_Z = Z(\tau) \rho_A \rho_B P_2$, $vk_{IC} = (A_i(\tau) \rho_A P_1)^n_{i=0}$
|
||||
|
||||
---
|
||||
|
||||
```go
|
||||
type Pk struct { // Proving Key pk:=(pkA, pkB, pkC, pkH)
|
||||
G1T [][3]*big.Int // t encrypted in G1 curve, G1T == Pk.H
|
||||
A [][3]*big.Int
|
||||
B [][3][2]*big.Int
|
||||
C [][3]*big.Int
|
||||
Kp [][3]*big.Int
|
||||
Ap [][3]*big.Int
|
||||
Bp [][3]*big.Int
|
||||
Cp [][3]*big.Int
|
||||
Z []*big.Int
|
||||
}
|
||||
|
||||
type Vk struct {
|
||||
Vka [3][2]*big.Int
|
||||
Vkb [3]*big.Int
|
||||
Vkc [3][2]*big.Int
|
||||
IC [][3]*big.Int
|
||||
G1Kbg [3]*big.Int // g1 * Kbeta * Kgamma
|
||||
G2Kbg [3][2]*big.Int // g2 * Kbeta * Kgamma
|
||||
G2Kg [3][2]*big.Int // g2 * Kgamma
|
||||
Vkz [3][2]*big.Int
|
||||
}
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
```go
|
||||
// Setup is the data structure holding the Trusted Setup data. The Setup.Toxic sub struct must be destroyed after the GenerateTrustedSetup function is completed
|
||||
type Setup struct {
|
||||
Toxic struct {
|
||||
T *big.Int // trusted setup secret
|
||||
Ka *big.Int
|
||||
Kb *big.Int
|
||||
Kc *big.Int
|
||||
Kbeta *big.Int
|
||||
Kgamma *big.Int
|
||||
RhoA *big.Int
|
||||
RhoB *big.Int
|
||||
RhoC *big.Int
|
||||
}
|
||||
Pk Pk
|
||||
Vk Vk
|
||||
}
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
## Proofs generation
|
||||
- $A, B, C, Z$ (from the QAP)
|
||||
- random $\delta_1, \delta_2, \delta_3$
|
||||
- $H(z)= \dfrac{A(z)B(z)-C(z)}{Z(z)}$
|
||||
- $A(z) = A_0(z) + \sum_{i=1}^m s_i A_i(x) + \delta_1 Z(z)$
|
||||
- $B(z) = B_0(z) + \sum_{i=1}^m s_i B_i(x) + \delta_2 Z(z)$
|
||||
- $C(z) = C_0(z) + \sum_{i=1}^m s_i B_i(x) + \delta_2 Z(z)$
|
||||
(where $m$ is the number of public inputs)
|
||||
|
||||
---
|
||||
|
||||
- $\pi_A = <c, pk_A>$
|
||||
- $\pi_A' = <c, pk_A'>$
|
||||
- $\pi_B = <c, pk_B>$
|
||||
- example:
|
||||
```go
|
||||
for i := 0; i < circuit.NVars; i++ {
|
||||
proof.PiB = Utils.Bn.G2.Add(proof.PiB, Utils.Bn.G2.MulScalar(pk.B[i], w[i]))
|
||||
proof.PiBp = Utils.Bn.G1.Add(proof.PiBp, Utils.Bn.G1.MulScalar(pk.Bp[i], w[i]))
|
||||
}
|
||||
```
|
||||
($c=1+witness+\delta_1+\delta_2+\delta_3$
|
||||
- $\pi_B' = <c, pk_B'>$
|
||||
- $\pi_C = <c, pk_C>$
|
||||
- $\pi_C' = <c, pk_C'>$
|
||||
- $\pi_K = <c, pk_K>$
|
||||
- $\pi_H = <h, pk_KH>$
|
||||
- proof: $\pi = (\pi_A, \pi_A', \pi_B, \pi_B', \pi_C, \pi_C', \pi_K, \pi_H$
|
||||
|
||||
---
|
||||
|
||||
## Proofs verification
|
||||
|
||||
<img src="imgs/cat03.jpeg" style="float:right; width:300px;" />
|
||||
|
||||
- $vk_{kx} = vk_{IC,0} + \sum_{i=1}^n x_i vk_{IC,i}$
|
||||
|
||||
Verification:
|
||||
- $e(\pi_A, vk_a) == e(\pi_{A'}, g_2)$
|
||||
- $e(vk_b, \pi_B) == e(\pi_{B'}, g_2)$
|
||||
- $e(\pi_C, vk_c) == e(\pi_{C'}, g_2)$
|
||||
- $e(vk_{kx}+\pi_A, \pi_B) == e(\pi_H, vk_{kz}) \cdot e(\pi_C, g_2)$
|
||||
- $e(vk_{kx} + \pi_A + \pi_C, V_{\beta\gamma}^2) \cdot e(vk_{\beta\gamma}^1, \pi_B) == e(\pi_k, vk_{\gamma}^1)$
|
||||
|
||||
---
|
||||
|
||||
|
||||
<div style="font-size:60%">
|
||||
Example (whiteboard):
|
||||
<br><br>
|
||||
|
||||
$\dfrac{
|
||||
e(\pi_A, \pi_B)
|
||||
}{
|
||||
e(\pi_C, g_2)
|
||||
}
|
||||
= e(g_1 h(t), g_2 z(t))
|
||||
$
|
||||
<br>
|
||||
$\dfrac{
|
||||
e(A_1 + A_2 + ... + A_n, B_1 + B_2 + ... + B_n)
|
||||
}{
|
||||
e(C_1 + C_2 + ... + C_n, g_2)
|
||||
}
|
||||
= e(g_1 h(t), g_2 z(t))
|
||||
$
|
||||
<br>
|
||||
$\dfrac{
|
||||
e(g_1 \alpha_1(t) s_1 + g_1 \alpha_2(t) s_2 + ... + g_1 \alpha_n(t) s_n, g_2 \beta_1(t)s_1 + g_2 \beta_2(t) s_2 + ... + g_2 \beta_n(t) s_n)
|
||||
}{
|
||||
e(g_1 \gamma_1(t) s_1 + g_1 \gamma_2(t) s_2 + ... + g_1 \gamma_n(t) s_n, g_2)
|
||||
}
|
||||
= e(g_1 h(t), g_2 z(t))
|
||||
$
|
||||
<br>
|
||||
$
|
||||
e(g_1 \alpha_1(t) s_1 + g_1 \alpha_2(t) s_2 + ... + g_1 \alpha_n(t) s_n, g_2 \beta_1(t)s_1 + g_2 \beta_2(t) s_2 + ... + g_2 \beta_n(t) s_n)$
|
||||
$= e(g_1 h(t), g_2 z(t)) \cdot e(g_1 \gamma_1(t) s_1 + g_1 \gamma_2(t) s_2 + ... + g_1 \gamma_n(t) s_n, g_2)
|
||||
$
|
||||
|
||||
</div>
|
||||
|
||||
|
||||
---
|
||||
|
||||
## Groth16
|
||||
|
||||
|
||||
<img src="imgs/cat02.jpeg" style="float:right; width:300px;" />
|
||||
|
||||
### Trusted Setup
|
||||
$\tau = \alpha, \beta, \gamma, \delta, x$
|
||||
|
||||
$\sigma_1 =$
|
||||
- $\alpha, \beta, \delta, \{ x^i\}_{i=0}^{n-1}$
|
||||
|
||||
- $\{
|
||||
\dfrac{
|
||||
\beta u_i(x) + \alpha v_i(x) + w_i(x)
|
||||
}{
|
||||
\gamma
|
||||
}
|
||||
\}_{i=0}^l$
|
||||
|
||||
- $\{
|
||||
\dfrac{
|
||||
\beta u_i(x) + \alpha v_i(x) + w_i(x)
|
||||
}{
|
||||
\delta
|
||||
}
|
||||
\}_{i=l+1}^m$
|
||||
|
||||
- $\{
|
||||
\dfrac{x^i t(x)}{\delta}
|
||||
\}_{i=0}^{n-2}$
|
||||
|
||||
$\sigma_2 = (\beta, \gamma, \delta, \{ x^i \}_{i=0}^{n-1})$
|
||||
|
||||
*(where $u_i(x), v_i(x), w_i(x)$ are the $QAP$)*
|
||||
|
||||
---
|
||||
|
||||
```go
|
||||
type Pk struct { // Proving Key
|
||||
BACDelta [][3]*big.Int // {( βui(x)+αvi(x)+wi(x) ) / δ } from l+1 to m
|
||||
Z []*big.Int
|
||||
G1 struct {
|
||||
Alpha [3]*big.Int
|
||||
Beta [3]*big.Int
|
||||
Delta [3]*big.Int
|
||||
At [][3]*big.Int // {a(τ)} from 0 to m
|
||||
BACGamma [][3]*big.Int // {( βui(x)+αvi(x)+wi(x) ) / γ } from 0 to m
|
||||
}
|
||||
G2 struct {
|
||||
Beta [3][2]*big.Int
|
||||
Gamma [3][2]*big.Int
|
||||
Delta [3][2]*big.Int
|
||||
BACGamma [][3][2]*big.Int // {( βui(x)+αvi(x)+wi(x) ) / γ } from 0 to m
|
||||
}
|
||||
PowersTauDelta [][3]*big.Int // powers of τ encrypted in G1 curve, divided by δ
|
||||
}
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
```go
|
||||
type Vk struct {
|
||||
IC [][3]*big.Int
|
||||
G1 struct {
|
||||
Alpha [3]*big.Int
|
||||
}
|
||||
G2 struct {
|
||||
Beta [3][2]*big.Int
|
||||
Gamma [3][2]*big.Int
|
||||
Delta [3][2]*big.Int
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
---
|
||||
|
||||
```go
|
||||
// Setup is the data structure holding the Trusted Setup data. The Setup.Toxic sub struct must be destroyed after the GenerateTrustedSetup function is completed
|
||||
type Setup struct {
|
||||
Toxic struct {
|
||||
T *big.Int // trusted setup secret
|
||||
Kalpha *big.Int
|
||||
Kbeta *big.Int
|
||||
Kgamma *big.Int
|
||||
Kdelta *big.Int
|
||||
}
|
||||
Pk Pk
|
||||
Vk Vk
|
||||
}
|
||||
```
|
||||
|
||||
---
|
||||
|
||||
#
|
||||
## Proofs Generation
|
||||
$\pi_A=\alpha + \sum_{i=0}^m \alpha_i u_i(x) + r \delta$
|
||||
$\pi_B=\beta + \sum_{i=0}^m \alpha_i v_i(x) + s \delta$
|
||||
|
||||
<div style="font-size:80%;">
|
||||
|
||||
$\pi_C = \dfrac{
|
||||
\sum_{i=l+1}^m a_i(\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x)t(x)
|
||||
}{
|
||||
\delta
|
||||
} + \pi_As + \pi_Br -rs\delta$
|
||||
|
||||
</div>
|
||||
|
||||
$\pi=\pi_A^1, \pi_B^1, \pi_C^2$
|
||||
|
||||
---
|
||||
|
||||
### Proof Verification
|
||||
|
||||
<div style="font-size:75%;">
|
||||
|
||||
$[\pi_A]_1 \cdot [\pi_B]_2 = [\alpha]_1 \cdot [\beta]_2 +
|
||||
\sum_{i=0}^l a_i [
|
||||
\dfrac{
|
||||
\beta u_i(x) + \alpha v_i(x) + w_i(x)
|
||||
}{
|
||||
\gamma
|
||||
}
|
||||
]_1
|
||||
\cdot [\gamma]_2 + [\pi_C]_1 \cdot [\delta]_2
|
||||
$
|
||||
|
||||
</div>
|
||||
|
||||
$e(\pi_A, \pi_B) = e(\alpha, \beta) \cdot e(pub, \gamma) \cdot e(\pi_C, \delta)$
|
||||
|
||||
|
||||
---
|
||||
|
||||
## How we use zkSNARKs in iden3
|
||||
- proving a credentials without revealing it's content
|
||||
- proving that an identity has a claim issued by another identity, without revealing all the data
|
||||
- proving any property of an identity
|
||||
- $ITF$ (Identity Transition Function), a way to prove with a zkSNARK that an identity has been updated following the defined protocol
|
||||
- identities can not cheat when issuing claims
|
||||
- etc
|
||||
|
||||
## Other ideas for free time side project
|
||||
- Zendermint (Tendermint + zkSNARKs)
|
||||
|
||||
---
|
||||
|
||||
|
||||
<img src="imgs/cat05.jpeg" style="float:right; width:300px;" />
|
||||
|
||||
## zkSNARK libraries
|
||||
- [bellman](https://github.com/zkcrypto/bellman) (rust)
|
||||
- [libsnark](https://github.com/scipr-lab/libsnark) (c++)
|
||||
- [snarkjs](https://github.com/iden3/snarkjs) (javascript)
|
||||
- [websnark](https://github.com/iden3/websnark) (wasm)
|
||||
- [go-snark](https://github.com/arnaucube/go-snark) (golang) <span style="font-size:80%;">[do not use in production]<span>
|
||||
|
||||
## Circuit languages
|
||||
| language | snark library with which plugs in |
|
||||
|-----|-----|
|
||||
| [Zokrates](https://github.com/Zokrates/ZoKrates) | libsnark, bellman |
|
||||
| [Snarky](https://github.com/o1-labs/snarky) | libsnark |
|
||||
| [circom](https://github.com/iden3/circom) | snarkjs, websnark, bellman |
|
||||
| [go-snark-circuit](https://github.com/arnaucube/go-snark) | go-snark |
|
||||
|
||||
---
|
||||
|
||||
## Utilities (Elliptic curve & Hash functions) inside the zkSNARK
|
||||
- we work over $F_r$, where $r=$`21888242871839275222246405745257275088548364400416034343698204186575808495617`
|
||||
|
||||
- BabyJubJub
|
||||
- Mimc
|
||||
- Poseidon
|
||||
|
||||
---
|
||||
|
||||
##### *Utilities (Elliptic curve & Hash functions) inside the zkSNARK*
|
||||
|
||||
### BabyJubJub
|
||||
- explaination: https://medium.com/zokrates/efficient-ecc-in-zksnarks-using-zokrates-bd9ae37b8186
|
||||
- implementations:
|
||||
- go: https://github.com/iden3/go-iden3-crypto
|
||||
- javascript & circom: https://github.com/iden3/circomlib
|
||||
- rust: https://github.com/arnaucube/babyjubjub-rs
|
||||
- c++: https://github.com/barryWhiteHat/baby_jubjub_ecc
|
||||
|
||||
---
|
||||
|
||||
##### *Utilities (Elliptic curve & Hash functions) inside the zkSNARK*
|
||||
|
||||
### Mimc7
|
||||
- explaination: https://eprint.iacr.org/2016/492.pdf
|
||||
- implementations in:
|
||||
- go: https://github.com/iden3/go-iden3-crypto
|
||||
- javascript & circom: https://github.com/iden3/circomlib
|
||||
- rust: https://github.com/arnaucube/mimc-rs
|
||||
|
||||
---
|
||||
|
||||
##### *Utilities (Elliptic curve & Hash functions) inside the zkSNARK*
|
||||
|
||||
### Poseidon
|
||||
- explaination: https://eprint.iacr.org/2019/458.pdf
|
||||
- implementations in:
|
||||
- go: https://github.com/iden3/go-iden3-crypto
|
||||
- javascript & circom: https://github.com/iden3/circomlib
|
||||
|
||||
---
|
||||
|
||||
# References
|
||||
- `Succinct Non-Interactive Zero Knowledge for a von Neumann Architecture`, Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, Madars Virza https://eprint.iacr.org/2013/879.pdf
|
||||
- `Pinocchio: Nearly practical verifiable computation`, Bryan Parno, Craig Gentry, Jon Howell, Mariana Raykova https://eprint.iacr.org/2013/279.pdf
|
||||
- `On the Size of Pairing-based Non-interactive Arguments`, Jens Groth https://eprint.iacr.org/2016/260.pdf
|
||||
- (also all the links through the slides)
|
||||
|
||||
---
|
||||
|
||||
<div style="text-align:center;">
|
||||
Thank you very much
|
||||
<br>
|
||||
<img src="imgs/cat00.jpeg" style="width:300px;" />
|
||||
</div>
|
||||
|
||||
|
||||
<div style="float:right; text-align:right;">
|
||||
<img style="width:80px" src="imgs/arnaucube.png" /> <br>
|
||||
|
||||
[arnaucube.com](https://arnaucube.com)
|
||||
[github.com/arnaucube](https://github.com/arnaucube)
|
||||
[twitter.com/arnaucube](https://twitter.com/arnaucube)
|
||||
|
||||
<a href="https://creativecommons.org/licenses/by-nc-sa/4.0/"><img src="https://licensebuttons.net/l/by-nc-sa/4.0/88x31.png" /></a>
|
||||
2019-08-20
|
||||
</div>
|
||||
|
||||
<img style="width:200px;" src="imgs/iden3.png" /> <br>
|
||||
[iden3.io](https://iden3.io)
|
||||
[github.com/iden3](https://github.com/iden3)
|
||||
[twitter.com/identhree](https://twitter.com/identhree)
|
||||